题目内容
4.菱形的两条对角线长分别是6和$6\sqrt{3}$,则菱形的面积是18$\sqrt{3}$,周长是24.分析 如图,AC=6$\sqrt{3}$,BD=6,根据菱形的性质得AC⊥BD,A=OC=$\frac{1}{2}$AC=3$\sqrt{3}$,OB=OD=$\frac{1}{2}$BD=3,则利用勾股定理可计算出AB=6,然后根据菱形的面积公式和菱形的周长定义求解.
解答 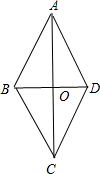 解:如图,AC=6$\sqrt{3}$,BD=6,
解:如图,AC=6$\sqrt{3}$,BD=6,
∵四边形ABCD为菱形,
∴AC⊥BD,A=OC=$\frac{1}{2}$AC=3$\sqrt{3}$,OB=OD=$\frac{1}{2}$BD=3,
在Rt△AOB中,AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{3}^{2}+(3\sqrt{3})^{2}}$=6,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6$\sqrt{3}$×6=18$\sqrt{3}$,菱形ABCD的周长=4AB=4×6=24.
故答案为18$\sqrt{3}$,24.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积等于对角线乘积的一半.

练习册系列答案
相关题目
17. 如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )
如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )
 如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )
如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
9.下列算式中,正确的是( )
| A. | (a2b3)5÷(ab2)10=ab5 | B. | ($\frac{1}{3}$)-2=$\frac{1}{3^2}$=$\frac{1}{9}$ | ||
| C. | (0.00001)0=(9999)0 | D. | 3.24×10-4=0.0000324 |
13.如果一个三角形的两个外角之和为270°,那么这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=147.5°.
如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=147.5°.