题目内容
10. 如图所示,沿DE折叠矩形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,求CE的长.
如图所示,沿DE折叠矩形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,求CE的长.
分析 首先由AD=8,且△AFD的面积为60,求得AF的长,然后由勾股定理求得DE的长,继而可求得AB,CD的长,然后设CE=x,由勾股定理即可求得方程:22+(8-x)2=x2,解此方程即可求得答案.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,BC=AD=8,
∵AD=8,△AFD的面积为60,
∴$\frac{1}{2}$AD•AF=60,
解得:AF=15,
∴DF=$\sqrt{A{D}^{2}+A{F}^{2}}$=17,
由折叠的性质可得:AB=CD=DF=17,EF=CE,
∴BF=AB-AF=17-15=2,
设CE=x,则EF=CE=x,BE=BC-CE=8-x,
在Rt△BEF中,BF2+BE2=EF2,
∴22+(8-x)2=x2,
解得:x=$\frac{17}{4}$,
∴CE=$\frac{17}{4}$.
点评 此题考查了折叠的性质、矩形的性质以及勾股定理.注意首先求得DF的长,再利用方程思想的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.抛掷一枚质地均匀的硬币,连续3次都是正面向上,则关于第4次抛掷结果,下面叙述正确的是( )
| A. | P(正面向上)>P(反面向上) | B. | P(正面向上)<P(反面向上) | ||
| C. | P(正面向上)=P(反面向上) | D. | 无法确定 |
2.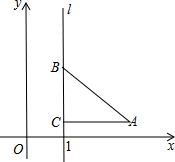 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
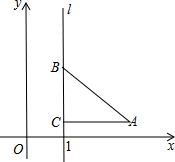 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )| A. | 3 | B. | 6 | C. | 12 | D. | $\frac{15}{4}$ |
20.若a>b,则下列不等式一定成立的是( )
| A. | a+b>b | B. | $\frac{b}{a}$>1 | C. | ac2>bc2 | D. | b-a<0 |
 如图,三角形ABC的三条边的长都是2个单位,现将三角形ABC沿射线BC方向向右平移1个单位后,得到三角形DEF,则四边形ABFD的周长为8个单位.
如图,三角形ABC的三条边的长都是2个单位,现将三角形ABC沿射线BC方向向右平移1个单位后,得到三角形DEF,则四边形ABFD的周长为8个单位. 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF=9.
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF=9.