题目内容
 在Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,EF∥AC.求证:AB=BF.
在Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,EF∥AC.求证:AB=BF.考点:全等三角形的判定与性质
专题:证明题
分析:由AB⊥AC,AD⊥BC,利用同角的余角相等得到一对角相等,再由EF与AC平行,得到一对同位角相等,等量代换得到∠3=∠EFB,再由BE为角平分线得到一对角相等,BE为公共边,利用AAS得到三角形ABE与三角形FBE全等,利用全等三角形对应边相等即可得证.
解答:证明:∵∠BAC=90°,AD⊥BC,
∴∠3+∠ABC=∠C+∠ABC=90°,
∴∠3=∠C,
∵EF∥AC,
∴∠C=∠EFB,
∴∠EFB=∠3,
∵BE平分∠ABC,
∴∠1=∠2,
在△ABE和△BFE中,
,
∴△ABE≌△BFE(AAS),
∴AB=BF.
∴∠3+∠ABC=∠C+∠ABC=90°,
∴∠3=∠C,
∵EF∥AC,
∴∠C=∠EFB,
∴∠EFB=∠3,
∵BE平分∠ABC,
∴∠1=∠2,
在△ABE和△BFE中,
|
∴△ABE≌△BFE(AAS),
∴AB=BF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列根式中,属同类二次根式的是( )
A、5
| |||||
B、
| |||||
C、
| |||||
D、
|
若方程ax2+bx+c=0(a≠0)中,a,b,c满足a+b+c=0和a-b+c=0,则方程的根是( )
| A、x1=1,x2=O |
| B、x1=-1,x2=O |
| C、x1=1,x2=-1 |
| D、无法确定 |
 如图,已知点D在△ABC的BC边上且与点B、C不重合,过点D作AC的平行线交AB于E,作AB的平行线交AC于F,BC=10.如果AC=
如图,已知点D在△ABC的BC边上且与点B、C不重合,过点D作AC的平行线交AB于E,作AB的平行线交AC于F,BC=10.如果AC= 如图,四边形ABCD中,AB=BC,AB∥CD,∠D=90°,AE⊥BC于点E,求证:CD=CE.
如图,四边形ABCD中,AB=BC,AB∥CD,∠D=90°,AE⊥BC于点E,求证:CD=CE. 在平行四边形ABCD中,对角线AC和BD相交于点O,AD⊥BD,AC=2
在平行四边形ABCD中,对角线AC和BD相交于点O,AD⊥BD,AC=2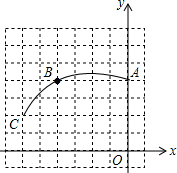 如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作: