题目内容
12.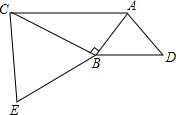 如图,△ABC中,∠ABC=90°,以AB、BC分别作等边△ABD和等边△BCE,求证:BD⊥CE.
如图,△ABC中,∠ABC=90°,以AB、BC分别作等边△ABD和等边△BCE,求证:BD⊥CE.
分析 首先根据等边三角形的性质得出∠ECB=∠ABD=60°,作BF∥CE,交AC于E,根据平行线的性质得出∠FBC=∠ECB=60°,进而求得∠ABF=30°,得出∠DBF=∠ABF+∠ABD=30°+60°=90°,最即可判断出BD⊥CE.
解答 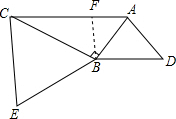 解:∵△BCE和△ABD是等边三角形,
解:∵△BCE和△ABD是等边三角形,
∴∠ECB=∠ABD=60°,
作BF∥CE,交AC于E,
∴∠CBF=∠ECB=60°,
∵∠ABC=90°,
∴∠ABF=30°,
∴∠DBF=∠ABF+∠ABD=30°+60°=90°,
∴BD⊥BF,
∵BF∥CE,
∴BD⊥CE.
点评 此题考查了等边三角形的性质和应用,作出平行线线,应用平行线的性质求得∠CBF=∠ECB=60°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.对于非零的两个实数a、b,规定a?b=2b-a,若1?(x+1)=1,则x的值为( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | 0 |
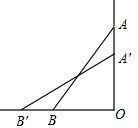 如图,一架长2.5m的梯子,斜放在墙上,梯子的底部B离墙角O的距离是0.7m,当梯子的顶部A向下滑0.4m到A′时,梯子的底部向外移动0.8m.
如图,一架长2.5m的梯子,斜放在墙上,梯子的底部B离墙角O的距离是0.7m,当梯子的顶部A向下滑0.4m到A′时,梯子的底部向外移动0.8m.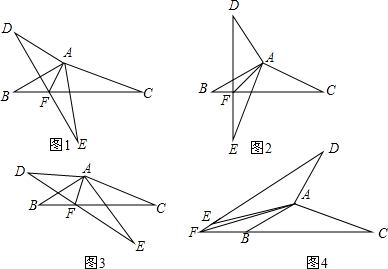
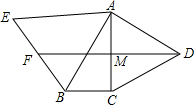 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.