题目内容
5.不等式组$\left\{\begin{array}{l}{2x+3<7}\\{5x-6<9}\end{array}\right.$的解是( )| A. | 2<x<3 | B. | x>3或x<2 | C. | 无解 | D. | x<2 |
分析 分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}{2x+3<7①}\\{5x-6<9②}\end{array}\right.$
由①得x<2,
由②得x<3,
故原不等式组的解集为x<2.
故选:D.
点评 本题考查的是解一元一此不等式组,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
20.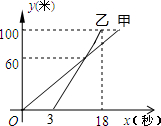 甲、乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )
甲、乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )
 甲、乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )
甲、乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )| A. | 离终点40米处,乙追上甲 | B. | 甲比乙迟3秒到终点 | ||
| C. | 甲跑步的速度是5米/秒 | D. | 乙跑步的速度是$\frac{20}{3}$米/秒 |
10.下列说法:①已知a=8-b,c2=ab-16,则a=b;②已知a=22015,b=(-2)2015,则4a2-8ab+4b2=22034;③已知a+b=3,ab=-1,则a4+b4=45.其中正确的是( )
| A. | ①②③ | B. | ①② | C. | ① | D. | ② |
17.设b>0,二次函数y=ax2+bx+a2-1的图象为下列之一,则a的值为( )
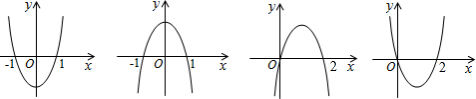
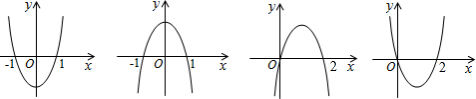
| A. | -1 | B. | 1 | C. | $\frac{-1-\sqrt{5}}{2}$ | D. | $\frac{-1+\sqrt{5}}{2}$ |
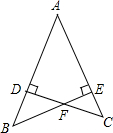 已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.
已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.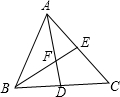 如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.
如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.