题目内容
7.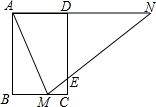 如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E (1)求证:△AMN是等腰三角形;
(2)求BM•AN的最大值;
(3)当M为BC中点时,求ME的长.
分析 (1)根据矩形的性质和平行线的性质证明即可;
(2)作NH⊥AM于H,证明△NAH∽△AMB,根据相似三角形的性质得到AN•BM=$\frac{1}{2}$AM2,根据勾股定理计算即可;
(3)由(2)的结论,结合相似三角形的性质求出CE,根据勾股定理计算即可.
解答 (1)证明:∵四边形ABCD是矩形,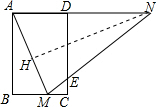
∴AD∥BC,
∴∠NAM=∠BMA,又∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)解:作NH⊥AM于H,
∵AN=MN,NH⊥AM,
∴AH=$\frac{1}{2}$AM,
∵∠NHA=∠ABM=90°,∠AMN=∠AMB,
∴△NAH∽△AMB,
∴$\frac{AN}{AM}$=$\frac{AH}{BM}$,
∴AN•BM=AH•AM=$\frac{1}{2}$AM2,
在Rt△AMB中,AM2=AB2+BM2=9+BM2,
∵BM≤2,
∴9+BM2≤13,
∴AN•BM≤$\frac{13}{2}$,
即当BM=2时,BM•AN的最大值为$\frac{13}{2}$;
(3)解:∵M为BC中点,
∴BM=CM=$\frac{1}{2}$BC=1,
由(2)得,AN•BM=$\frac{1}{2}$AM2,
∵AM2=32+12=10,
∴AN=5,
∴DN=5-2=3,
设DE=x,则CE=3-x,
∵AN∥BC,
∴$\frac{DN}{CM}$=$\frac{DE}{CE}$,即$\frac{3}{1}$=$\frac{x}{3-x}$,
解得,x=$\frac{9}{4}$,即DE=$\frac{9}{4}$,
∴CE=$\frac{3}{4}$,
∴ME=$\sqrt{C{E}^{2}+C{M}^{2}}$=$\frac{5}{4}$.
点评 本题考查的是相似三角形的判定和性质、勾股定理的应用以及等腰三角形的性质和矩形的性质,掌握相似三角形的判定定理和性质定理是解题的关键,注意方程思想的正确运用.

 名校课堂系列答案
名校课堂系列答案| A. | -10 | B. | -2 | C. | 2 | D. | 10 |
| A. | x<3 | B. | 3<x<5 | C. | x>5 | D. | 无解 |
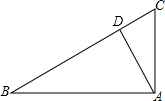 如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )| A. | 10cm | B. | 7.5cm | C. | 8.5cm | D. | 6.5cm |
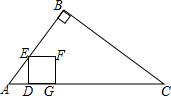 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).