题目内容
11．
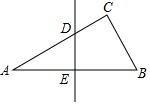如图，△ABC中，∠C=90°，∠A=30°，AB的垂直平分线交AC于D，交AB于E，CD=1，则AC=3．
分析 连接BD，根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，等边对等角可得∠ABD=∠A，再求出∠BCD=30°，根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2CD，再根据AC=AD+CD代入数据计算即可得解．
解答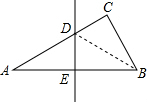 
解：如图，连接BD，
∵DE垂直平分AB，
∴AD=BD，
∴∠ABD=∠A=30°，
∵∠C=90°，
∴∠BCD=90°-30°-30°=30°，
∴BD=2CD=2×1=2，
∴AC=AD+CD=2+1=3．
故答案为：3．
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟记各性质是解题的关键．
练习册系列答案
相关题目
2．与$\sqrt{2}$-$\sqrt{3}$互为倒数的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$ | B． | $\sqrt{2}$-$\sqrt{3}$ | C． | $\sqrt{3}$-$\sqrt{2}$ | D． | -$\sqrt{2}$-$\sqrt{3}$ |
19．若不等式ax＜5的解集是x＞-1，则a的值为（ ）
| A． | -15 | B． | -5 | C． | -6 | D． | -9 |
16．下列各式中正确的是（ ）
| A． | -2a3•3a2=-6a5 | B． | 3a2•4a2=12a2 | C． | （a+1）（a-1）=a2-a+1 | D． | a15÷a3=a5（a≠0） |
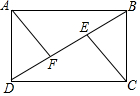如图，在四边形ABCD中，E，F是对角线BD上两点，其中AD∥BC，∠DAF=∠BCE，AD=BC．求证：AB∥CD．