ΧβΡΩΡΎ»ί
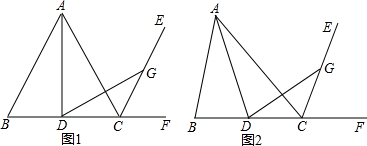
 »γΆΦΘ§≈ΉΈοœΏy=-x2+2x+3”κx÷αœύΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§ΕΞΒψΈΣDΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷αDF”κBCœύΫΜ”ΎΒψEΘ§”κx÷αœύΫΜ”ΎΒψFΘ°
»γΆΦΘ§≈ΉΈοœΏy=-x2+2x+3”κx÷αœύΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§ΕΞΒψΈΣDΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷αDF”κBCœύΫΜ”ΎΒψEΘ§”κx÷αœύΫΜ”ΎΒψFΘ°Θ®1Θ©«σœΏΕΈDEΒΡ≥ΛΘΜ
Θ®2Θ©…ηΙΐEΒΡ÷±œΏ”κ≈ΉΈοœΏœύΫΜ”ΎΒψMΘ®x1Θ§y1Θ©Θ§NΘ®x2Θ§y2Θ©Θ§ ‘≈–ΕœΒ±|x1-x2|ΒΡ÷ΒΉν–Γ ±Θ§÷±œΏMN”κx÷αΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©…ηPΈΣx÷α…œΒΡ“ΜΒψΘ§ΓœDAO+ΓœDPO=ΓœΠΝΘ§Β±tanΓœΠΝ=4 ±Θ§«σΒψPΒΡΉχ±ξΘ°
ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ¥ζ ΐΉέΚœΧβ,―Ι÷αΧβ
Ζ÷ΈωΘΚΘ®1Θ©ΗυΨί≈ΉΈοœΏΒΡΫβΈω ΫΦ¥Ω…«σΒΟ”κΉχ±ξ÷αΒΡΉχ±ξΦΑΕΞΒψΉχ±ξΘ§ΫχΕχ«σΒΟ÷±œΏBCΒΡΫβΈω ΫΘ§Α―Ε‘≥Τ÷α¥ζ»κ÷±œΏBCΒΡΫβΈω ΫΦ¥Ω…«σΒΟΘ°
Θ®2Θ©…η÷±œΏMNΒΡΫβΈω ΫΈΣy=kx+bΘ§“άΨίEΘ®1Θ§2Θ©ΒΡΉχ±ξΦ¥Ω…±μ Ψ≥ω÷±œΏMNΒΡΫβΈω Ϋy=Θ®2-bΘ©x+bΘ§ΗυΨί÷±œΏMNΒΡΫβΈω ΫΚΆ≈ΉΈοœΏΒΡΫβΈω ΫΦ¥Ω…«σΒΟx2-bx+b-3=0Θ§Υυ“‘x1+x2=bΘ§x1 x2=b-3ΘΜΗυΨίΆξ»ΪΤΫΖΫΙΪ ΫΦ¥Ω…«σΒΟΓΏ|x1-x2|=
=
=
=
Θ§Υυ“‘Β±b=2 ±Θ§|x1-x2|Ήν–Γ÷Β=2
Θ§“ρΈΣb=2 ±Θ§y=Θ®2-bΘ©x+b=2Θ§Υυ“‘÷±œΏMNΓΈx÷αΘ°
Θ®3Θ©”…DΘ®1Θ§4Θ©Θ§‘ρtanΓœDOF=4Θ§ΒΟ≥ωΓœDOF=ΓœΠΝΘ§»ΜΚσΗυΨί»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ Φ¥Ω…«σΒΟΓœDPO=ΓœADOΘ§ΫχΕχ«σΒΟΓςADPΓΉΓςAODΘ§ΒΟ≥ωAD2=AO•APΘ§¥”Εχ«σΒΟOPΒΡ≥ΛΘ§ΫχΕχ«σΒΟPΒψΉχ±ξΘ°
Θ®2Θ©…η÷±œΏMNΒΡΫβΈω ΫΈΣy=kx+bΘ§“άΨίEΘ®1Θ§2Θ©ΒΡΉχ±ξΦ¥Ω…±μ Ψ≥ω÷±œΏMNΒΡΫβΈω Ϋy=Θ®2-bΘ©x+bΘ§ΗυΨί÷±œΏMNΒΡΫβΈω ΫΚΆ≈ΉΈοœΏΒΡΫβΈω ΫΦ¥Ω…«σΒΟx2-bx+b-3=0Θ§Υυ“‘x1+x2=bΘ§x1 x2=b-3ΘΜΗυΨίΆξ»ΪΤΫΖΫΙΪ ΫΦ¥Ω…«σΒΟΓΏ|x1-x2|=
| (x1-x2)2 |
| (x1+x2)2-4x1x2 |
| b2-4(b-3) |
| (b-2)2+8 |
| 2 |
Θ®3Θ©”…DΘ®1Θ§4Θ©Θ§‘ρtanΓœDOF=4Θ§ΒΟ≥ωΓœDOF=ΓœΠΝΘ§»ΜΚσΗυΨί»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ Φ¥Ω…«σΒΟΓœDPO=ΓœADOΘ§ΫχΕχ«σΒΟΓςADPΓΉΓςAODΘ§ΒΟ≥ωAD2=AO•APΘ§¥”Εχ«σΒΟOPΒΡ≥ΛΘ§ΫχΕχ«σΒΟPΒψΉχ±ξΘ°
Ϋβ¥πΘΚΫβΘΚ”…≈ΉΈοœΏy=-x2+2x+3Ω…÷ΣΘ§CΘ®0Θ§3Θ©Θ§
Ννy=0Θ§‘ρ-x2+2x+3=0Θ§ΫβΒΟΘΚx=-1Θ§x=3Θ§
ΓύAΘ®-1Θ§0Θ©Θ§BΘ®3Θ§0Θ©ΘΜ
ΓύΕΞΒψx=1Θ§y=4Θ§Φ¥DΘ®1Θ§4Θ©ΘΜ
ΓύDF=4
…η÷±œΏBCΒΡΫβΈω ΫΈΣy=kx+bΘ§¥ζ»κBΘ®3Θ§0Θ©Θ§CΘ®0Θ§3Θ©ΒΟΘΜ
Θ§ΫβΒΟ
Θ§
ΓύΫβΈω ΫΈΣΘΜy=-x+3Θ§
Β±x=1 ±Θ§y=-1+3=2Θ§
ΓύEΘ®1Θ§2Θ©Θ§
ΓύEF=2Θ§
ΓύDE=DF-EF=4-2=2Θ°
Θ®2Θ©…η÷±œΏMNΒΡΫβΈω ΫΈΣy=kx+bΘ§
ΓΏEΘ®1Θ§2Θ©Θ§
Γύ2=k+bΘ§
Γύk=2-bΘ§
Γύ÷±œΏMNΒΡΫβΈω Ϋy=Θ®2-bΘ©x+bΘ§
ΓΏΒψMΓΔNΒΡΉχ±ξ «
ΒΡΫβΘ§
’ϊάμΒΟΘΚx2-bx+b-3=0Θ§
Γύx1+x2=bΘ§x1x2=b-3ΘΜ
ΓΏ|x1-x2|=
=
=
=
Θ§
ΓύΒ±b=2 ±Θ§|x1-x2|Ήν–Γ÷Β=2
Θ§
ΓΏb=2 ±Θ§y=Θ®2-bΘ©x+b=2Θ§
Γύ÷±œΏMNΓΈx÷αΘ°
Θ®3Θ©»γΆΦ2Θ§ΓΏDΘ®1Θ§4Θ©Θ§

ΓύtanΓœDOF=4Θ§
”÷ΓΏtanΓœΠΝ=4Θ§
ΓύΓœDOF=ΓœΠΝΘ§
ΓΏΓœDOF=ΓœDAO+ΓœADO=ΓœΠΝΘ§
ΓΏΓœDAO+ΓœDPO=ΓœΠΝΘ§
ΓύΓœDPO=ΓœADOΘ§
ΓύΓςADPΓΉΓςAODΘ§
ΓύAD2=AO•APΘ§
ΓΏAF=2Θ§DF=4Θ§
ΓύAD2=AF2+DF2=20Θ§
ΓύOP=19Θ§
Ά§άμΘ§Β±ΒψP‘Ύ‘≠ΒψΉσ≤ύΘ§OP=17Θ°
ΓύP1Θ®19Θ§0Θ©Θ§P2Θ®-17Θ§0Θ©Θ°
Ννy=0Θ§‘ρ-x2+2x+3=0Θ§ΫβΒΟΘΚx=-1Θ§x=3Θ§
ΓύAΘ®-1Θ§0Θ©Θ§BΘ®3Θ§0Θ©ΘΜ
ΓύΕΞΒψx=1Θ§y=4Θ§Φ¥DΘ®1Θ§4Θ©ΘΜ
ΓύDF=4
…η÷±œΏBCΒΡΫβΈω ΫΈΣy=kx+bΘ§¥ζ»κBΘ®3Θ§0Θ©Θ§CΘ®0Θ§3Θ©ΒΟΘΜ
|
|
ΓύΫβΈω ΫΈΣΘΜy=-x+3Θ§
Β±x=1 ±Θ§y=-1+3=2Θ§
ΓύEΘ®1Θ§2Θ©Θ§
ΓύEF=2Θ§
ΓύDE=DF-EF=4-2=2Θ°
Θ®2Θ©…η÷±œΏMNΒΡΫβΈω ΫΈΣy=kx+bΘ§
ΓΏEΘ®1Θ§2Θ©Θ§
Γύ2=k+bΘ§
Γύk=2-bΘ§
Γύ÷±œΏMNΒΡΫβΈω Ϋy=Θ®2-bΘ©x+bΘ§
ΓΏΒψMΓΔNΒΡΉχ±ξ «
|
’ϊάμΒΟΘΚx2-bx+b-3=0Θ§
Γύx1+x2=bΘ§x1x2=b-3ΘΜ
ΓΏ|x1-x2|=
| (x1-x2)2 |
| (x1+x2)2-4x1x2 |
| b2-4(b-3) |
| (b-2)2+8 |
ΓύΒ±b=2 ±Θ§|x1-x2|Ήν–Γ÷Β=2
| 2 |
ΓΏb=2 ±Θ§y=Θ®2-bΘ©x+b=2Θ§
Γύ÷±œΏMNΓΈx÷αΘ°
Θ®3Θ©»γΆΦ2Θ§ΓΏDΘ®1Θ§4Θ©Θ§

ΓύtanΓœDOF=4Θ§
”÷ΓΏtanΓœΠΝ=4Θ§
ΓύΓœDOF=ΓœΠΝΘ§
ΓΏΓœDOF=ΓœDAO+ΓœADO=ΓœΠΝΘ§
ΓΏΓœDAO+ΓœDPO=ΓœΠΝΘ§
ΓύΓœDPO=ΓœADOΘ§
ΓύΓςADPΓΉΓςAODΘ§
ΓύAD2=AO•APΘ§
ΓΏAF=2Θ§DF=4Θ§
ΓύAD2=AF2+DF2=20Θ§
ΓύOP=19Θ§
Ά§άμΘ§Β±ΒψP‘Ύ‘≠ΒψΉσ≤ύΘ§OP=17Θ°
ΓύP1Θ®19Θ§0Θ©Θ§P2Θ®-17Θ§0Θ©Θ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥ¥ΐΕ®œΒ ΐΖ®«σΫβΈω ΫΘ§Εΰ¥ΈΚ· ΐΒΡΫΜΒψΓΔΕΞΒψΉχ±ξΓΔΕ‘≥Τ÷αΘ§“‘ΦΑœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®ΦΑ–‘÷ Θ§«σΒΟ»ΐΫ«–ΈœύΥΤ «±ΨΧβΒΡΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 »γΆΦΘ§Μ≠≥ωΓςOABœρœ¬ΤΫ“Τ4ΗωΒΞΈΜ≥ΛΕ»ΓΔ‘ΌœρΉσΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»ΚσΒΡΓςO1A1B1Θ°
»γΆΦΘ§Μ≠≥ωΓςOABœρœ¬ΤΫ“Τ4ΗωΒΞΈΜ≥ΛΕ»ΓΔ‘ΌœρΉσΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»ΚσΒΡΓςO1A1B1Θ°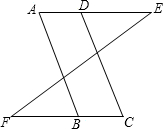 »γΆΦΘ§‘ΎΘΚΔΌABΓΈCDΘΜΔΎADΓΈBCΘΜΔέΓœA=ΓœC÷–Θ§«κΡψ―Γ»ΓΤδ÷–ΒΡΝΫΗωΉςΈΣΧθΦΰΘ§Νμ“ΜΗωΉςΈΣΫα¬έΘ§–¥≥ω“ΜΗω’ΐ»ΖΟϋΧβΘ§≤Δ÷ΛΟςΤδ’ΐ»Ζ–‘Θ°
»γΆΦΘ§‘ΎΘΚΔΌABΓΈCDΘΜΔΎADΓΈBCΘΜΔέΓœA=ΓœC÷–Θ§«κΡψ―Γ»ΓΤδ÷–ΒΡΝΫΗωΉςΈΣΧθΦΰΘ§Νμ“ΜΗωΉςΈΣΫα¬έΘ§–¥≥ω“ΜΗω’ΐ»ΖΟϋΧβΘ§≤Δ÷ΛΟςΤδ’ΐ»Ζ–‘Θ° »γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§CDΓΆABΘ§¥ΙΉψΈΣDΘ§‘ρΓœAΒΡ”ύΫ« «
»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§CDΓΆABΘ§¥ΙΉψΈΣDΘ§‘ρΓœAΒΡ”ύΫ« « »γΆΦΘ§ΓœACD=ΓœBCDΘ§DEΓΈBCΫΜAC”ΎEΘ°»τΓœACB=60ΓψΘ§ΓœB=74ΓψΘ§‘ρΓœEDC=
»γΆΦΘ§ΓœACD=ΓœBCDΘ§DEΓΈBCΫΜAC”ΎEΘ°»τΓœACB=60ΓψΘ§ΓœB=74ΓψΘ§‘ρΓœEDC=