题目内容
已知△ABC,AB=BC,D为边BC上任意一点,射线CE在∠ACF的内部,DG交CE于点G.
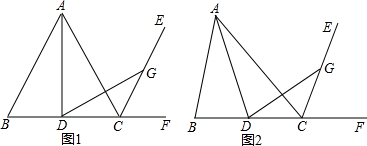
(1)如图1,若AB=AC,∠ECF=∠ADG=60°,试探究线段AD与线段DG的数量关系,写出你的结论,并加以证明;
(2)如图2,若∠B=∠ADG,请你给∠ECF补充一个条件,使得你在(1)中得到的结论仍然成立,并加以证明.

(1)如图1,若AB=AC,∠ECF=∠ADG=60°,试探究线段AD与线段DG的数量关系,写出你的结论,并加以证明;
(2)如图2,若∠B=∠ADG,请你给∠ECF补充一个条件,使得你在(1)中得到的结论仍然成立,并加以证明.
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)先判断出△ABC是等边三角形,根据等边三角形的性质可得∠ACD=∠ABF=60°,再求出∠ACE=60°,从而得到∠ADG=∠ACE,然后证明点A、D、C、G四点共圆,再根据同弧所对的圆周角相等可得∠DGA=∠ACD=60°,再求出∠DAG=60°,然后根据等角对等边可得AD=DG;
(2)根据(1)的思路,∠ECF=∠BAC,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACE=∠B,然后求出点A、D、C、G四点共圆,再根据同弧所对的圆周角相等求出∠AGD=∠ACB,根据三角形的内角和表示出∠ACB=∠DAG,从而得到∠DAG=∠AGD,再根据等角对等边证明即可.
(2)根据(1)的思路,∠ECF=∠BAC,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACE=∠B,然后求出点A、D、C、G四点共圆,再根据同弧所对的圆周角相等求出∠AGD=∠ACB,根据三角形的内角和表示出∠ACB=∠DAG,从而得到∠DAG=∠AGD,再根据等角对等边证明即可.
解答:证明:(1)∵AB=BC,AB=AC,
∴△ABC是等边三角形,
∴∠ACD=∠ABF=60°,
∵∠ECF=60°,
∴∠ACE=180°-60°×2=60°,
∴∠ADG=∠ACE,
∴点A、D、C、G四点共圆,
∴∠DGA=∠ACD=60°,
又∵∠DAG=180°-∠ADG-∠DGA=180°-60°-60°=60°,
∴∠DAG=∠DGA=60°,
∴AD=DG;
(2)∠ECF=∠BAC.
理由如下:由三角形的外角性质,∠ACE+∠ECF=∠BAC+∠B,
∵∠ECF=∠BAC,
∴∠ACE=∠B,
∵∠B=∠ADG,
∴∠ADG=∠ACE,
∴点A、D、C、G四点共圆,
∴∠AGD=∠ACB,
∵∠DAG=180°-∠ADG-∠AGD=180°-∠B-∠ACB=∠BAC,
∴∠ACB=∠DAG,
∴∠DAG=∠AGD=∠ACB,
∴AD=DG.
∴△ABC是等边三角形,
∴∠ACD=∠ABF=60°,
∵∠ECF=60°,
∴∠ACE=180°-60°×2=60°,
∴∠ADG=∠ACE,
∴点A、D、C、G四点共圆,
∴∠DGA=∠ACD=60°,
又∵∠DAG=180°-∠ADG-∠DGA=180°-60°-60°=60°,
∴∠DAG=∠DGA=60°,
∴AD=DG;

(2)∠ECF=∠BAC.
理由如下:由三角形的外角性质,∠ACE+∠ECF=∠BAC+∠B,
∵∠ECF=∠BAC,
∴∠ACE=∠B,
∵∠B=∠ADG,
∴∠ADG=∠ACE,
∴点A、D、C、G四点共圆,
∴∠AGD=∠ACB,
∵∠DAG=180°-∠ADG-∠AGD=180°-∠B-∠ACB=∠BAC,
∴∠ACB=∠DAG,
∴∠DAG=∠AGD=∠ACB,
∴AD=DG.
点评:本题考查了全等三角形的判定与性质,等腰三角形的性质,四点共圆的证明与应用,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质求出四点共圆并理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
图象经过二、三、四象限的一次函数是( )
| A、y=-x-1 |
| B、y=-x+1 |
| C、y=x-1 |
| D、y=x+1 |

 如图,∠AED=∠ACB,∠DEB=∠GFC,BE⊥AC,求证:FG⊥AC.
如图,∠AED=∠ACB,∠DEB=∠GFC,BE⊥AC,求证:FG⊥AC. 富平县是全国有名的奶山羊养殖基地,如图A、B、C为三个村庄,现准备建一个奶站M,使得奶站到三个村庄的距离相等,请你帮忙确定一下奶站M的位置,要求利用尺规作图,保留作图痕迹,不写作法.
富平县是全国有名的奶山羊养殖基地,如图A、B、C为三个村庄,现准备建一个奶站M,使得奶站到三个村庄的距离相等,请你帮忙确定一下奶站M的位置,要求利用尺规作图,保留作图痕迹,不写作法. 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点,与y轴交于点C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点,与y轴交于点C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.