题目内容
16.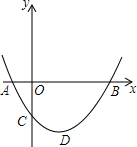 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3,与y轴负半轴交于点C.
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3,与y轴负半轴交于点C.(1)下列结论:①2a-b=0;②a+b+c>0;③c=-3a;其中正确的是③;
(2)若△ABD是等腰直角三角形,求a的值.
分析 (1)根据抛物线的对称轴是x=1,以及对称轴公式,当x=1时的函数值即可作出判断;
(2)作DE⊥AB于点E,根据△ABC是等腰直角三角形,即可求得D的坐标,利用待定系数法求得函数的解析式,从而求得a的值.
解答 解:(1)对称轴是x=$\frac{-1+3}{2}$=1,即-$\frac{b}{2a}$=1,则2a+b=0,故①错误;
当x=1时,y=a+b+c<0,故②错误;
∵函数经过点(-1,0)和(3,0),
∴$\left\{\begin{array}{l}{a-b+c=0…①}\\{9a+3b+c=0…②}\end{array}\right.$,
由①得b=a+c,
代入②得:9a+3(a+c)+c=0,即12a+4c=0,则c=-3a.故③正确.
故答案是:③;
(2)作DE⊥AB于点E.
AB=3-(-1)=4,
∵△ABC是等腰直角三角形,
∴DE=$\frac{1}{2}$AB=2,
则D的坐标是(1,-2).
设二次函数的解析式是y=a(x-1)2-2,
把(-1,0)代入得4a-2=0,
解得:a=$\frac{1}{2}$.
点评 本题考查了待定系数法求函数的解析式,正确根据等腰直角三角形的性质求得D的坐标是关键.

练习册系列答案
相关题目
7.下面四个图案中,不能由基本图案旋转得到的是( )
| A. |  | B. |  | C. |  | D. |  |
11.在我校初一新生的体操训练活动中,共有123名学生参加.假如将这123名学生排成一列,按1、2、3、4、3、2、1、2、3、4、3、2、1…的规律报数,那么最后一名学生所报的数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.某天早晨,小强从家出发,以一定的速度前往学校.途中在一饮食店吃早点,之后以一定的速度返回家中,下面的图象中表示小强从家到饮食店又回到家中的路程s(千米)与时间t(分钟)之间的关系的是( )
| A. |  | B. |  | C. |  | D. |  |
5.如果两个有理数的积是负数,和是正数,那么这两个有理数( )
| A. | 同号,且均为负数 | |
| B. | 异号,且正数的绝对值比负数的绝对值大 | |
| C. | 同号,且均为正数 | |
| D. | 异号,且负数的绝对值比正数的绝对值大 |
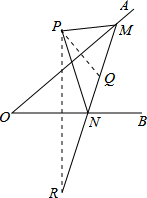 如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=3cm,PN=4cm,MN=4.5cm,则线段QR的长为5.5cm.
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=3cm,PN=4cm,MN=4.5cm,则线段QR的长为5.5cm.