题目内容
8.如果两个相似多边形面积的比为1:5,则它们的相似比为1:$\sqrt{5}$.分析 直接利用相似图形的性质由面积比得出相似比即可.
解答 解:∵两个相似多边形面积的比为1:5,
∴它们的相似比为:1:$\sqrt{5}$.
故答案为:1:$\sqrt{5}$.
点评 此题主要考查了相似多边形的性质,利用相似图形面积比等于相似比的平方求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.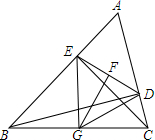 如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,则下列结论中错误的是( )
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,则下列结论中错误的是( )
 如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,则下列结论中错误的是( )
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,则下列结论中错误的是( )| A. | GE=GD | B. | GF⊥DE | C. | GF平分∠DGE | D. | ∠DGE=60° |
20.下列式子中,正确的是( )
| A. | $3(\overrightarrow a+2\overrightarrow b)=3\overrightarrow a+6\overrightarrow b$ | B. | $-(\overrightarrow a-\overrightarrow b)=-\overrightarrow a-\overrightarrow b$ | C. | $\overrightarrow 0+\overrightarrow a=\overrightarrow 0$ | D. | $0•\overrightarrow a=0$ |
18.下列运算结果正确的是( )
| A. | a6•a2=a12 | B. | (a6)2=a8 | C. | a6÷a2=a3 | D. | (ab)2=a2b2 |
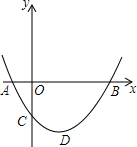 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3,与y轴负半轴交于点C.
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3,与y轴负半轴交于点C.