题目内容
6.多项式2x4-2x3+ax2+7x+b能被x2+x-2整除,求a、b的值和$\frac{a}{b}$的值(要求用列竖式的方法解答)分析 由多项式2x4-4x3+ax2+7x+b能被x2+x-2整除,得到2x4-4x3+ax2+7x+b=A(x2+x-2)=A(x-1)(x+2),把x=1与x=-2代入,使其值为0列出关于a与b的方程组,求出方程组的解得到a与b的值,进一步代入求出原式的值.
解答 解:∵多项式2x4-4x3+ax2+7x+b能被x2+x-2=(x-1)(x+2)整除,
∴2x4-4x3+ax2+7x+b=A(x2+x-2)=A(x-1)(x+2),
当x=1时,多项式为2-4+a+7+b=0,即a+b=-5;
当x=-2时,多项式为32+32+4a-14+b=0,即4a+b=-50,
解得:a=-15,b=10,
则$\frac{b}{a}$=$\frac{-15}{10}$=-$\frac{3}{2}$.
点评 此题考查了整式的除法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
15.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 7cm,5cm,12cm | B. | 6cm,8cm,15cm | C. | 4cm,6cm,5cm | D. | 8cm,4cm,3cm |
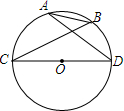 如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.
如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值. 如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.
如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC. 如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.
如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.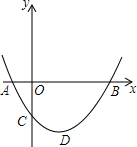 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3,与y轴负半轴交于点C.
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3,与y轴负半轴交于点C.