题目内容
10.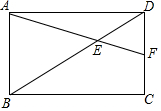 如图,在矩形ABCD中,AB=6,BC=8,点E在对角线BD上,且BE=6,连接AE并延长交DC于点F,则CF等于( )
如图,在矩形ABCD中,AB=6,BC=8,点E在对角线BD上,且BE=6,连接AE并延长交DC于点F,则CF等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据勾股定理求出BD,得到DE的长,根据相似三角形的性质得到比例式,代入计算即可求出DF的长,求出CF的长度.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,
又AB=CD=6,BC=AD=8,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10,
∵BE=6,
∴DE=10-6=4,
∵AB∥CD,
∴$\frac{DF}{AB}$=$\frac{DE}{BE}$,即$\frac{DF}{6}$=$\frac{4}{6}$,
解得,DF=4,
则CF=CD-DF=6-4=2,
故选:A.
点评 本题考查的是矩形的性质、相似三角形的判定和性质,掌握矩形的性质定理和相似三角形的判定定理、性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.张老师到移动公司办理下个月的手机套餐业务,有以下四种套餐可供选择,经过统计,张老师每月使用手机国内数据流量约800M,国内电话约150分钟,为使下月手机付费额最少,张老师应选择的套餐是( )
注:1G=1024M.
| 套餐内包含内容 | 套餐外资费 | |||
| 月费(元/月) | 国内数据流量 | 国内电话(分钟) | 流量 | 国内电话 |
| 58 | 500M | 50 | 0.29元/M | 0.19元/分钟 |
| 88 | 700M | 200 | ||
| 128 | 1G | 420 | ||
| 158 | 2G | 510 | ||
| A. | 58元/月 | B. | 88元/月 | C. | 128元/月 | D. | 158元/月 |
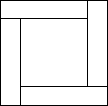
15. 小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
 小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )| A. | ①② | B. | ?①③ | C. | ③④ | D. | ?②④ |
2.己知线段AB的长为2,点P是线段AB的黄金分割点,且AP>PB,那么AP=( )
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
 小明同学用四张长为x,宽为y的长方形卡片,拼出如图所示的包含两个正方形的图形(任意两张相邻的卡片之间没有重叠,没有空隙).
小明同学用四张长为x,宽为y的长方形卡片,拼出如图所示的包含两个正方形的图形(任意两张相邻的卡片之间没有重叠,没有空隙).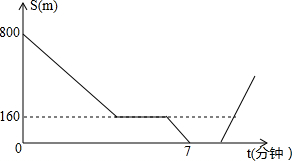 在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.
在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.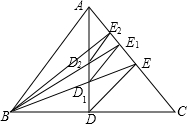 如图,在△ABC中,AB=AC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D;过D1,作D1E1∥AB于E1,连接BE1交AD于D1,过D2作D2E2∥AB于E2,…,如此继续,记S△BDE为S1,S${\;}_{△B{D}_{1}{E}_{1}}$记为S2,S${\;}_{△B{D}_{2}{E}_{2}}$记为S3,…,若S△ABC面积为1,则S2=$\frac{1}{9}$;Sn=$\frac{1}{(n+1)^{2}}$(用含n代数式表示).
如图,在△ABC中,AB=AC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D;过D1,作D1E1∥AB于E1,连接BE1交AD于D1,过D2作D2E2∥AB于E2,…,如此继续,记S△BDE为S1,S${\;}_{△B{D}_{1}{E}_{1}}$记为S2,S${\;}_{△B{D}_{2}{E}_{2}}$记为S3,…,若S△ABC面积为1,则S2=$\frac{1}{9}$;Sn=$\frac{1}{(n+1)^{2}}$(用含n代数式表示).