题目内容
2. 如图,△ABC为等边三角形,边长为2,AB与x轴平行,顶点C坐标为(2,$\sqrt{3}$+1),规定把等边△ABC“先沿x轴翻折,再向右平移1个单位”为一次变换,如果这样连续经过3次变换后,等边△ABC的顶点A的坐标为(4,-1),如果这样连续经过2017次变换后,等边△ABC的顶点A的坐标为(2018,-1).
如图,△ABC为等边三角形,边长为2,AB与x轴平行,顶点C坐标为(2,$\sqrt{3}$+1),规定把等边△ABC“先沿x轴翻折,再向右平移1个单位”为一次变换,如果这样连续经过3次变换后,等边△ABC的顶点A的坐标为(4,-1),如果这样连续经过2017次变换后,等边△ABC的顶点A的坐标为(2018,-1).
分析 据轴对称判断出点A变换后在x轴下方,然后求出点A纵坐标,再根据平移的距离求出点A变换后的横坐标,最后写出即可.
解答 解:∵顶点C坐标为(2,$\sqrt{3}$+1),△ABC为等边三角形,边长为2,
∴点C到x轴的距离为$\sqrt{3}$+1,横坐标为2,
∴A(1,1),
第3次变换后的三角形在x轴下方,
点A的纵坐标为-1,
横坐标为1+3=4,
所以,点A的对应点A′的坐标是(4,-1),
第2017次变换后的三角形在x轴下方,
点A的纵坐标为-1,
横坐标为1+2017×1=2018,
所以,点A的对应点A″的坐标是(2018,-1),
故答案为:(4,-1),(2018,-1).
点评 本题考查了坐标与图形变化-平移,等边三角形的性质,读懂题目信息,确定出连续2017次这样的变换得到三角形在x轴下方是解题的关键.

练习册系列答案
相关题目
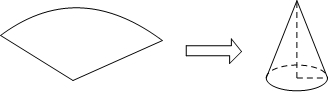
7.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的底面周长是( )

| A. | 2π cm | B. | 3π cm | C. | 4π cm | D. | 5π cm |
11. 某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
表一:
(1)根据表一的信息,请在表二中填写滚动的距离s(单位:米)的对应值,(提示:本题中,s=$\overline{v}$×x,$\overline{v}$=$\frac{{v}_{0}+{v}_{x}}{2}$,其中,v0表示开始时的速度,vx表示x秒时的速度.)
表二:
(2)根据表二中的数据在给出的平面坐标系中画出相应的点;
(3)选择适当的函数表示s与x之间的关系,求出相应的函数解析式;
(4)当s=13.75时,求滚动时间x.
 某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:表一:
| 时间x(秒) | 0 | 1 | 2 | 2.5 | 3 | … |
| 速度v(米/秒) | 8 | 6 | 4 | 3 | 2 | … |
表二:
| 时间x(秒) | 0 | 1 | 2 | 3 | … |
| 距离s(米) | 0 | … |
(3)选择适当的函数表示s与x之间的关系,求出相应的函数解析式;
(4)当s=13.75时,求滚动时间x.
12.已知x=-1,y=2是二元一次方程组3x+2y=m,nx-y=1的解,则m-n的值是( )
| A. | 0 | B. | -2 | C. | 1 | D. | 4 |
