题目内容
12．若$\frac{x}{y}$=$\frac{4}{5}$，则$\frac{2x-y}{x+y}$的值为$\frac{1}{3}$．分析 根据等式的性质，可用y表示x，根据分式的性质，可得答案．
解答 解：由$\frac{x}{y}$=$\frac{4}{5}$，得
x=$\frac{4}{5}$y．
$\frac{2x-y}{x+y}$=$\frac{2×\frac{4}{5}y-y}{\frac{4}{5}y+y}$=$\frac{\frac{3}{5}y}{\frac{9}{5}y}$=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$．
点评 本题考查了比例的性质，利用等式的性质得出x=$\frac{4}{5}$y是解题关键．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
（1）如图，工人师傅要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，使其圆心在线段AC上，且与AB、BC都相切．请你在图中画出这个半圆．（要求用直尺和圆规作图，保留作图痕迹，不要求写作法）．
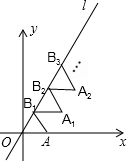如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为1的等边三角形，点A在x轴上，点O，B1，B2，B3，…都在直线l上，则点A2016的坐标是（1009，1008$\sqrt{3}$）．