题目内容
9.△ABC中,AB=AC=17,BC=16,则△ABC的面积120.分析 利用等腰三角形的性质求得BD=$\frac{1}{2}$BC=8cm.然后在直角△ABD中,利用勾股定理来求AD的长度,进而可求出三角形的面积.
解答 解:如图,作AD⊥BC于点D,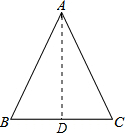
∵△ABC中,AB=AC=17,BC=16,
∴BD=$\frac{1}{2}$BC=8,
∴在直角△ABD中,由勾股定理,得AD=$\sqrt{1{7}^{2}-{8}^{2}}$=15,
∴S△ABC=$\frac{1}{2}$×15×16=120,
故答案为:120.
点评 此题主要考查了勾股定理,等腰三角形的性质的理解及运用.利用等腰三角形“三线合一”的性质求得AD的长度是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
19.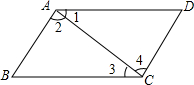 如图,下列判断错误的是( )
如图,下列判断错误的是( )
 如图,下列判断错误的是( )
如图,下列判断错误的是( )| A. | 如果∠2=∠4,那么AB∥CD | B. | 如果∠1=∠3,那么AB∥CD | ||
| C. | 如果∠BAD+∠D=180,那么AB∥CD | D. | 如果∠BAD+∠B=180,那么AD∥CD |
18.下列运算正确的是( )
| A. | 3m4÷m3=3m2 | B. | m+m2=m3 | C. | (m+n)(m-n)=m2-n2 | D. | ($\frac{m}{2}$)3=$\frac{{m}^{3}}{2}$ |
 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为24+8$\sqrt{5}$.
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为24+8$\sqrt{5}$.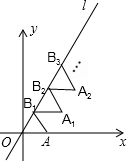 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).