题目内容
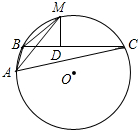 如图,
如图, |
| AC |
 |
| AC |
 |
| AM |
考点:圆周角定理,全等三角形的判定与性质,等腰三角形的判定与性质,圆心角、弧、弦的关系
专题:证明题
分析:首先在CD上取点N,使CN=AB,连接CM,MN,然后证明△ABM≌△CNM,从而得到BM=MN,再根据等腰三角形的性质可得BD=ND,进而可得AB+BD=DC.
解答: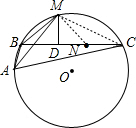 证明:在CD上取点N,使CN=AB,连接CM,MN
证明:在CD上取点N,使CN=AB,连接CM,MN
∵M是
的中点,
∴
=
,
∴AM=CM(等弧对等弦),
又∵∠BAM=∠BCM,
在△ABM和△CNM中,
,
∴△ABM≌△CNM(SAS),
∴BM=MN,
∴△BMN为等腰三角形(BN为底),
又∵MD⊥BN,
∴D为BN中点(等腰三角形三线合一),
∴BD=DN
∴AB+BD=CD.
 证明:在CD上取点N,使CN=AB,连接CM,MN
证明:在CD上取点N,使CN=AB,连接CM,MN∵M是
 |
| AC |
∴
 |
| AM |
 |
| CM |
∴AM=CM(等弧对等弦),
又∵∠BAM=∠BCM,
在△ABM和△CNM中,
|
∴△ABM≌△CNM(SAS),
∴BM=MN,
∴△BMN为等腰三角形(BN为底),
又∵MD⊥BN,
∴D为BN中点(等腰三角形三线合一),
∴BD=DN
∴AB+BD=CD.
点评:此题主要考查了圆周角定理,以及全等三角形的判定与性质,关键是正确作出辅助线.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
如果代数式7a3-6a2b+5a3+ma2b的值与b无关,则( )
| A、a=0 | B、b=0 |
| C、m=0 | D、m=6 |
在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③(x-2)(x+5)=x2-1;④3x2-
=0.
①3x2+7=0;②ax2+bx+c=0;③(x-2)(x+5)=x2-1;④3x2-
| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
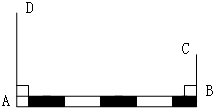 如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.
如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.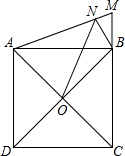 如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为
如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为