题目内容
16. 如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )| A. | x<-5 | B. | x>-5 | C. | x>7 | D. | x<-7 |
分析 kx+b>0可看作是函数y=kx+b的函数值大于0,然后观察图象得到图象在x轴上方,对应的自变量的取值范围为x>-2,这样即可得到不等式kx+b>0的解集.
解答 解:根据题意,kx+b>0,
即函数y=kx+b的函数值大于0,图象在x轴上方,对应的自变量的取值范围为x>-5,
故不等式kx+b>0的解集是:x>-5.
故选:B.
点评 本题考查了一次函数与一元一次不等式:对于一次函数y=kx+b,当y>0时对应的自变量的取值范围为不等式kx+b>0的解集.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
4.某种药品原价为35元/盒,经过连续两次降价后售价为26元/盒,设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A. | 35(1-x)2=35-26 | B. | 35(1-2x)=26 | C. | 35(1-x)2=26 | D. | 35(1-x2)=26 |
8.通过统计甲、乙、丙、丁四名同学某学期的四次数学测试成绩,得到甲、乙、丙、丁三明同学四次数学测试成绩的方差分别为S甲2=17,S乙2=36,S丙2=14,丁同学四次数学测试成绩(单位:分)
如下表:
则这四名同学四次数学测试成绩最稳定的是( )
如下表:
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 丁同学 | 80 | 80 | 90 | 90 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
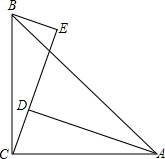 如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.
如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.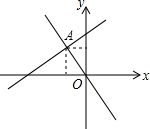 如图,函数y=-2x和y=kx+4的图象相交于点A(m,3),则关于的x不等式kx+4+2x≥0的解集为x≥-1.5.
如图,函数y=-2x和y=kx+4的图象相交于点A(m,3),则关于的x不等式kx+4+2x≥0的解集为x≥-1.5. A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t.
A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t.
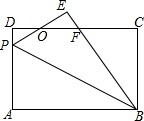 如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )
如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )