题目内容
6.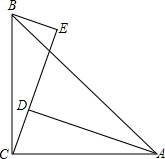 如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.
如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.
分析 先证明△BCE≌△CAD,得BE=CD=0.8,CE=AD=2.5,然后根据线段和差定义即可解决.
解答 解:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∴∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠BCE=∠CAD,
∴△BCE≌△CAD,
∴CD=BE=0.8cm,CE=AD=2.5cm,
∴DE=CD-CE,=2.5-0.8=1.7 cm.
点评 本题考查全等三角形的判定和性质、熟练掌握全等三角形的判定和性质是解决问题的关键,学会正确寻找全等三角形,属于中考常考题型.

练习册系列答案
相关题目
1.在${\frac{1}{x}}、{\frac{1}{3}}、{\frac{{{x^2}+1}}{2}}、{\frac{5+y}{π}}、\frac{{{a^2}+1}}{a^2}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.若一元二次方程x2-2x-m=0无实数根,则二次函数y=(m+1)x2+m-1的图象必经过第( )象限.
| A. | 一、二 | B. | 三、四 | C. | 一、二、三 | D. | 一、三、四 |
16. 如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
 如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )| A. | x<-5 | B. | x>-5 | C. | x>7 | D. | x<-7 |

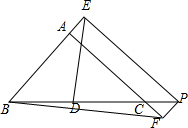 如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.
如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.