题目内容
4.某种药品原价为35元/盒,经过连续两次降价后售价为26元/盒,设平均每次降价的百分率为x,根据题意所列方程正确的是( )| A. | 35(1-x)2=35-26 | B. | 35(1-2x)=26 | C. | 35(1-x)2=26 | D. | 35(1-x2)=26 |
分析 可先表示出第一次降价后的价格,那么第一次降价后的价格×(1-降低的百分率)=26,把相应数值代入即可求解.
解答 解:第一次降价后的价格为35×(1-x),两次连续降价后售价在第一次降价后的价格的基础上降低x,为35×(1-x)×(1-x),
则列出的方程是35(1-x)2=26.
故选C.
点评 考查由实际问题抽象出一元二次方程中求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
相关题目
15.若一元二次方程x2-2x-m=0无实数根,则二次函数y=(m+1)x2+m-1的图象必经过第( )象限.
| A. | 一、二 | B. | 三、四 | C. | 一、二、三 | D. | 一、三、四 |
12.若关于x,y的方程组$\left\{\begin{array}{l}{5x+3ay=16}\\{-bx+4y=15}\end{array}\right.$(其中a,b是常数)的解为$\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$,则方程组 $\left\{\begin{array}{l}{5(x+1)+3a(x-2y)=16}\\{-b(x+1)+4(x-2y)=15}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5.5}\\{y=-1}\end{array}\right.$ |
19.点M(-3,-5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为( )
| A. | (0,-9) | B. | (-6,-1) | C. | (1,-2) | D. | (1,-8) |
9.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16. 如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
 如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )| A. | x<-5 | B. | x>-5 | C. | x>7 | D. | x<-7 |
10.用10米长的铝材制成一个矩形窗框,使它的面积为6平方米,若设它的一条边长为x米,则根据题意可列出的关于x的方程为( )
| A. | x(10÷2+x)=6 | B. | x(10÷2-x)=6 | C. | x(10-x)=6 | D. | x(x-1)=28 |
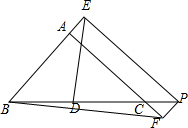 如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.
如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.