题目内容
20.对于任意非零实数a、b,定义运算“⊕”,使下列式子成立:1⊕2=-$\frac{3}{2}$,2⊕1=$\frac{3}{2}$,(-2)⊕5=$\frac{21}{10}$,5⊕(-2)=-$\frac{21}{10}$,…,则(-3)⊕(-4)=( )| A. | -$\frac{7}{12}$ | B. | $\frac{7}{12}$ | C. | -$\frac{25}{12}$ | D. | $\frac{25}{12}$ |
分析 根据已知数字等式得出变化规律,最后将-3和-4代入根据规律进行计算即可.
解答 解:1⊕2=-$\frac{3}{2}$=$\frac{{1}^{2}-{2}^{2}}{1×2}$;
2⊕1=$\frac{3}{2}$=$\frac{{2}^{2}-{1}^{2}}{1×2}$;
(-2)⊕5=$\frac{21}{10}$=$\frac{(-2)^{2}-{5}^{2}}{(-2)×5}$
5⊕(-2)=-$\frac{21}{10}$=$\frac{{5}^{2}-(-2)^{2}}{5×(-2)}$
…
a⊕b=$\frac{{a}^{2}-{b}^{2}}{ab}$.
∴(-3)⊕(-4)=$\frac{(-3)^{2}-(-4)^{2}}{(-3)×(-4)}$=-$\frac{7}{12}$.
故选:A.
点评 此题主要考查了数字变化规律,根据已知得出数字中的变与不变是解题关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
10.下列调查中,适合采用全面调查的事件是( )
| A. | 国家旅游局调查国民对“五一”期间出行旅游的满意程度 | |
| B. | 了解湖南卫视“我是歌手”总决赛在全国的收视率 | |
| C. | 调查重庆市初2015级学生的心理健康状况 | |
| D. | 调查你班上的同学是否计划在暑假期间参与社会实践活动 |
8.“低碳生活,绿色出行”,电动汽车将逐渐代替燃油汽车,成为人们出行的主要交通工具,某城市一汽车销售4S店,今年2月份销售电动汽车共计64辆,4月份销售电动汽车共计100辆.若每月汽车销售增长率相同,则该汽车销售4S店5月份能销售电动汽车( )辆.
| A. | 111 | B. | 118 | C. | 125 | D. | 132 |
15.分解因式:y3-4y2+4y=( )
| A. | y(y2-4y+4) | B. | y(y-2)2 | C. | y(y+2)2 | D. | y(y+2)(y-2) |
5.某电子产品经过11月、12月连续两次降价,售价由3900元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )
| A. | 3900(1+x)2=2500 | B. | 3900(1-x)2=2500 | C. | 3900(1-2x)=2500 | D. | 2500(1+x)2=3900 |
12.把ax2-4ay2分解因式正确的是( )
| A. | a(x+2y)(x-2y) | B. | a(x-2y)2 | C. | a(x-4y)2 | D. | a(x+4y)(x-4y) |
 如图,边长为1的正六边形ABCDEF内接于⊙O,则图中阴影部分图形的面积是$\frac{π}{3}$(结果保留π)
如图,边长为1的正六边形ABCDEF内接于⊙O,则图中阴影部分图形的面积是$\frac{π}{3}$(结果保留π)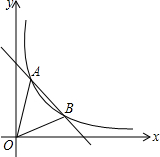 如图,已知A(-1,2),B(m,1)是一次函数y=-x+b的图象和反比例函数y=$\frac{2}{x}$(x>0)的图象的两个交点,连结AO,BO.
如图,已知A(-1,2),B(m,1)是一次函数y=-x+b的图象和反比例函数y=$\frac{2}{x}$(x>0)的图象的两个交点,连结AO,BO.