题目内容
17．
如图，⊙O的半径为5，弦心距OC=3，则弦AB的长是（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 5 |
分析 先根据垂径定理得出AB=2AC，再根据勾股定理求出AD的长，进而得出AB的长．
解答 解：连接OA，如图所示：
∵OC⊥AB，OC=3，OA=5，
∴AB=2AC，
∵AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴AB=2AC=8．
故选C．
点评 本题考查的是垂径定理及勾股定理；熟练掌握垂径定理，由勾股定理求出AC是解决问题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
3．计算$\sqrt{2\frac{1}{4}}$的结果是（ ）
| A． | $\frac{3}{2}$ | B． | $±2\frac{1}{2}$ | C． | $±\frac{3}{2}$ | D． | 2$\frac{1}{2}$ |
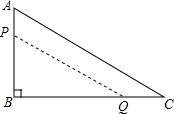如图，在ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动，动点Q从点B开始沿边BC向C以4mm/s的速度移动，如果P、Q分别从A、B同时出发，那么PBQ的面积S随出发时间t如何变化？写出函数关系式及t的取值范围．
9．若$\sqrt{{a}^{2}}=（\sqrt{a}）^{2}$，则a的取值范围是（ ）
| A． | a≥0 | B． | a≠0 | C． | a＜0 | D． | a为任意实数 |
6．已知关于x的一元二次方程x2-2x-k=0的一个根为3，则它的另一个根为（ ）
| A． | -5 | B． | -1 | C． | 1 | D． | 5 |
在如图所示的2016年1月份的月历表中，用一个3×2的长方形框围住相邻三列两行中的6个数字，设其中第一行中间的数字为x．