题目内容
3.关于x、y的方程组$\left\{\begin{array}{l}{3x+2y=m+3}\\{2x-y=2m-1}\end{array}\right.$的解中,①若y≤0,求m的取值范围;
②若x>y,求m的取值范围.
分析 ①把m看做已知数表示出y,根据y≤0求出m的范围即可;
②表示出x与y,根据x>y,求出m的范围即可.
解答 解:①$\left\{\begin{array}{l}{3x+2y=m+3①}\\{2x-y=2m-1②}\end{array}\right.$,
①×2-②×3得:7y=-4m+9,即y=$\frac{-4m+9}{7}$,
①+②×2得:7x=5m+1,即x=$\frac{5m+1}{7}$,
由题意得:$\frac{-4m+9}{7}$≤0,
解得:m≥$\frac{9}{4}$;
②根据题意得:$\frac{5m+1}{7}$>$\frac{-4m+9}{7}$,
解得:m>$\frac{8}{9}$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
18.一次函数y=ax+b,当x<5时,y>7,那么不等式ax+b>7的解集为( )
| A. | x<5 | B. | x>5 | C. | x≥5 | D. | x≤5 |
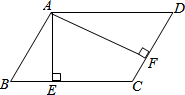 已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长.
已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长. 如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.
如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.