题目内容
11.解方程:|2x-1|+|x-2|=|x+1|.分析 根据绝对值的性质分几种情况进行简化方程解答即可.
解答 解:当x≤-1时,原方程可化为:1-2x-2+x=-1-x,
解得:x≤-1的实数;
当$-1≤x≤\frac{1}{2}$时,原方程可化为:1-2x-2+x=x+1,
解得:x=-1,
当$\frac{1}{2}≤x≤2$时,原方程可化为:2x-1-x+2=x+1,
解得:x取$\frac{1}{2}≤x≤2$的实数;
当x≥2时,原方程可化为:2x-1+x-2=x+1,
解得:x=2.
点评 本题主要考查的是含有绝对值符号的一元一次方程的一般计算.难易适中.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
2.下列说法中,错误的是( )
| A. | 不等式x<5的解有无数多个 | B. | 不等式x<5的正整数解有有限个 | ||
| C. | 不等式-3x>9的解是x<-3 | D. | 35是不等式2x<-16的一个解 |
6.如图所示,∠2和∠1是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
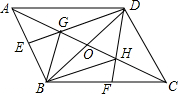 如图,已知G,H是△ABC的边AC的等分点,GE∥BH交AB于E,HF∥BG交BC于F,延长EG、FH交于D点,连接AD、DC、BD.设AC和BD交于O点,求证:四边形ABCD是平行四边形.
如图,已知G,H是△ABC的边AC的等分点,GE∥BH交AB于E,HF∥BG交BC于F,延长EG、FH交于D点,连接AD、DC、BD.设AC和BD交于O点,求证:四边形ABCD是平行四边形.