题目内容
10.计算tan1°•tan2°•tan3°•…•tan88°•tan89°=1.分析 根据一个角的正切函数等于它余角的余切函数,根据同一个正切乘以余切的乘积为1,可得答案.
解答 解:原式=cot89°•cot88°•cot87°•cot86°•…•tan86°•tan87°•tan88°•tan89°
=(tan89°•cot89°)•(tan88°•cot88°)•(tan87°•cot87°)•tan45°
=1.
故答案为:1.
点评 本题考查了互余两角三角函数的关系,利用一个角的正切函数等于它余角的余切函数是解题关键.

练习册系列答案
相关题目
1.二次根式$\sqrt{a-b}$的有理化因式是( )
| A. | $\sqrt{a+b}$ | B. | $\sqrt{a}$+$\sqrt{b}$ | C. | $\sqrt{a-b}$ | D. | $\sqrt{a}$-$\sqrt{b}$ |
5.若$\sqrt{{(a-4)}^{2}}$=a-4,则a的取值范围是( )
| A. | a<4 | B. | a≤4 | C. | a>4 | D. | a≥4 |
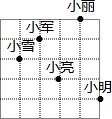 如图,是阳光小区内的一幢商品房示意图,如小军家所在的位置用(2,4)表示.
如图,是阳光小区内的一幢商品房示意图,如小军家所在的位置用(2,4)表示. 已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.
已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c. 2015年8月5日,河南省长恒县第一中学发布了体育看台建设项目施工招标的公告,该看台的部分侧面示意图如图所示,该看台每个台阶的高度都相等,线段MN表示的是看台上方的遮阳板.已知∠ACE=30°,CD=2$\sqrt{3}$m,DE=BN=1m,∠E=∠ADE=90°,MN∥CE.
2015年8月5日,河南省长恒县第一中学发布了体育看台建设项目施工招标的公告,该看台的部分侧面示意图如图所示,该看台每个台阶的高度都相等,线段MN表示的是看台上方的遮阳板.已知∠ACE=30°,CD=2$\sqrt{3}$m,DE=BN=1m,∠E=∠ADE=90°,MN∥CE. 如图所示,将一个含60°角的直角三角形按照如图放置在作业纸上,纸上横线是一组平行线,若∠1=20°,则∠2=50°.
如图所示,将一个含60°角的直角三角形按照如图放置在作业纸上,纸上横线是一组平行线,若∠1=20°,则∠2=50°.