题目内容
2. 2015年8月5日,河南省长恒县第一中学发布了体育看台建设项目施工招标的公告,该看台的部分侧面示意图如图所示,该看台每个台阶的高度都相等,线段MN表示的是看台上方的遮阳板.已知∠ACE=30°,CD=2$\sqrt{3}$m,DE=BN=1m,∠E=∠ADE=90°,MN∥CE.
2015年8月5日,河南省长恒县第一中学发布了体育看台建设项目施工招标的公告,该看台的部分侧面示意图如图所示,该看台每个台阶的高度都相等,线段MN表示的是看台上方的遮阳板.已知∠ACE=30°,CD=2$\sqrt{3}$m,DE=BN=1m,∠E=∠ADE=90°,MN∥CE.(1)求CF的高度;
(2)若MN=$\frac{4\sqrt{3}-3}{2}$m,求点M到点C的距离.
分析 (1)RT△ACD中,由∠ACD=30°知AC=2AD,再根据勾股定理可求得AD的长度,除以台阶数即可得;
(2)过点M作MP⊥CE于点P,连接MC,由题意可知MP=NE=AD+BN,CP=CE-PE=CE-MN,在RT△PCM中根据勾股定理可得MC长度.
解答 解:(1)在RT△ACD中,∵∠ACD=30°,
∴AC=2AD,
又∵AC2=AD2+CD2,且CD=2$\sqrt{3}$,
∴4AD2=AD2+12,解得:AD=2,
由图可知,共有5个台阶,
故CF=$\frac{1}{4}$AD=0.4m;
(2)过点M作MP⊥CE于点P,连接MC,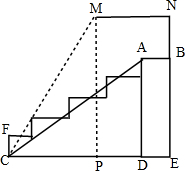
∴∠MPE=∠E=90°,
∴MP∥NE,
又∵MN∥CE,
∴四边形MNEP为矩形,
∴MP=NE=AB+BN=AD+BN=3m,
CP=CE-PE=CE-MN=2$\sqrt{3}$+1-$\frac{4\sqrt{3}-3}{2}$=$\frac{5}{2}$m,
在RT△PCM中,∵MC2=MP2+CP2,
∴MC=$\sqrt{{3}^{2}+(\frac{5}{2})^{2}}$=$\frac{\sqrt{61}}{2}$,
故点M到点C的距离为$\frac{\sqrt{61}}{2}$m.
点评 本题主要考查勾股定理及矩形的判定与性质,做垂直构建直角三角形根据勾股定理求斜边长度是切入点,根据矩形性质得出直角三角形直角边长是关键.

练习册系列答案
相关题目
17.下列命题中,是真命题的是( )
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 依次连接四边形四边中点所组成的图形是矩形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
7.八名学生参加初中英语听力口语自动化考试成绩如下:28,21,29,27,30,26,30,25.这组数据的平均数、极差分别是( )
| A. | 26、9 | B. | 27、9 | C. | 27、10 | D. | 28、10 |
14.下列剪纸图案中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.已知1,2,3,4,5的方差是2,则101,102,103,104,105的方差是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |