题目内容
10.已知∠AOB内一点C关于OA、OB的对称点分别为D、E,若∠AOB=30°,则△DOE是等边三角形.分析 根据题意画出草图,根据轴对称的性质求得OE=CO=OD,∠EOD=60°,即可判断△DOE为等边三角形.
解答 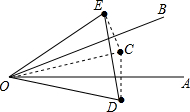 解:根据题意画出图形:
解:根据题意画出图形:
∵C关于OA、OB的对称点分别为D、E
∴AO⊥CD,CO=OD
BO⊥EC,OE=OC
∴△EOC为等腰三角形
△COD为等腰三角形
∴∠EOC=∠COB,∠COA=∠AOD,OE=OC=OD
又∵∠AOB=30°
∴∠BOC+∠AOC=30°
∴∠BOE+∠AOD=30°
∴∠EOD=60°
又∵EO=OD
∴△EOD为等边三角形.
故答案为:等边.
点评 本题考查了轴对称的性质以及等边三角形的判定及性质.关键要理解有一个角为60°的等腰三角形是等边三角形,其中60°可以是顶角,也可以是底角.

练习册系列答案
相关题目
5.下列说法正确的有( )
①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去.则第n个图形需要棋子( )

| A. | 4n枚 | B. | 4n-1枚 | C. | 3n+1枚 | D. | 3n-1枚 |
19.一个数的倒数是它本身,则这个数是( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 1或-1或0 |

 如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,F,M都在直线l上,且ME=MF,直线EA与直线OF交于点P.点M的坐标为(1,-1),点F的坐标为(1,1)时,
如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,F,M都在直线l上,且ME=MF,直线EA与直线OF交于点P.点M的坐标为(1,-1),点F的坐标为(1,1)时,