题目内容
 某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.
某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.| 次数 | 70≤x<90 | 90≤x<110 | 110≤x<130 | 130≤x<150 | 150≤x<170 |
| 人数 | 8 | 23 | 16 | 2 | 1 |
(1)本次调查的样本容量是
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有
(3)根据上表的数据补全直方图;
(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或树状图写出分析过程).
考点:频数(率)分布直方图,频数(率)分布表,列表法与树状图法
专题:图表型
分析:(1)根据图表给出的数据可直接得出本次调查的样本容量;
(2)把调查中每分钟跳绳次数达到110次以上(含110次)的人数加起来即可;
(3)根据图表给出的数据可直接补全直方图;
(4)根据题意画出树状图,得出抽中一男一女的情况,再根据概率公式,即可得出答案.
(2)把调查中每分钟跳绳次数达到110次以上(含110次)的人数加起来即可;
(3)根据图表给出的数据可直接补全直方图;
(4)根据题意画出树状图,得出抽中一男一女的情况,再根据概率公式,即可得出答案.
解答:解:(1)本次调查的样本容量是:8+23+16+2+1=50;
故答案为:50;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有人数是:
16+2+1=19(人);
故答案为:19;
(3)根据图表所给出的数据补图如下:

(4)根据题意画树状图如下:

共有6种情况,恰好抽中一男一女的有4种情况,
则恰好抽中一男一女的概率是
=
.
故答案为:50;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有人数是:
16+2+1=19(人);
故答案为:19;
(3)根据图表所给出的数据补图如下:

(4)根据题意画树状图如下:

共有6种情况,恰好抽中一男一女的有4种情况,
则恰好抽中一男一女的概率是
| 4 |
| 6 |
| 2 |
| 3 |
点评:此题考查了条形统计图和频数(率)分布直方图,用到的知识点是样本容量、概率公式,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
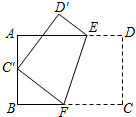 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )| A、4 | ||
B、3
| ||
| C、4.5 | ||
| D、5 |
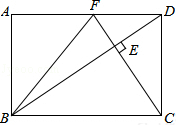 在矩形ABCD中,DC=2
在矩形ABCD中,DC=2 如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是
如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是