题目内容
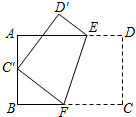如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上．若AB=6，BC=9，则BF的长为（ ）| A、4 | ||
B、3
| ||
| C、4.5 | ||
| D、5 |
考点：翻折变换（折叠问题）,勾股定理的应用
专题：
分析：先求出BC′，再由图形折叠特性知，C′F=CF=BC-BF=9-BF，在Rt△C′BF中，运用勾股定理BF2+BC′2=C′F2求解．
解答：解：∵点C′是AB边的中点，AB=6，
∴BC′=3，
由图形折叠特性知，C′F=CF=BC-BF=9-BF，
在Rt△C′BF中，BF2+BC′2=C′F2，
∴BF2+9=（9-BF）2，
解得，BF=4，
故选：A．
∴BC′=3，
由图形折叠特性知，C′F=CF=BC-BF=9-BF，
在Rt△C′BF中，BF2+BC′2=C′F2，
∴BF2+9=（9-BF）2，
解得，BF=4，
故选：A．
点评：本题考查了折叠问题及勾股定理的应用，综合能力要求较高．同时也考查了列方程求解的能力．解题的关键是找出线段的关系．
练习册系列答案
相关题目
如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在y轴上，点B1，B2，B3，…都在直线y=靖江市教育局为帮助全市贫困师生举行“一日捐”活动，甲、乙两校教师各捐款60000元，已知“…”，设乙学校教师有x人，则可得方程
-
=20，根据此情景，题中用“…”表示的缺失的条件应补（ ）
| 60000 |
| x |
| 60000 |
| (1+20%)x |
| A、乙校教师比甲校教师人均多捐20元，且甲校教师的人数比乙校教师的人数多20% |
| B、甲校教师比乙校教师人均多捐20元，且乙校教师的人数比甲校教师的人数多20% |
| C、甲校教师比乙校教师人均多捐20元，且甲校教师的人数比乙校教师的人数多20% |
| D、乙校教师比甲校教师人均多捐20元，且乙校教师的人数比甲校教师的人数多20% |
小军家距学校5千米，原来他骑自行车上学，学校为保障学生安全，新购进校车接送学生，若校车速度是他骑车速度的2倍，现在小军乘校车上学可以从家晚10分钟出发，结果与原来到校时间相同．设小军骑车的速度为x千米/小时，则所列方程正确的为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
为了调动员工的积极性，某家电商场的经理制定了新的工资分配方案．员工工资包括基本工资和奖励工资．若设员工每月的销售额为x元，该月可得工资为y元．则y（元）和x（元）之间的函数图象如图．
某校为了了解学生大课间活动的跳绳情况，随机抽取了50名学生每分钟跳绳的次数进行统计，把统计结果绘制成如表和直方图．