Question

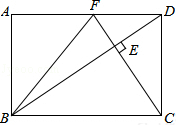在矩形ABCD中，DC=2

3

，F为AD的中点，CF⊥BD分别交BD、AD于点E、F，连接BF．
（1）求证：△DEC∽△FDC；
（2）求sin∠FBD的值；
（3）求BC的长度．

Answer 1

考点：相似三角形的判定与性质,矩形的性质

专题：

分析：（1）由在矩形ABCD中，CF⊥BD，可得∠DEC=∠FDC=90°，又由∠DCE=∠FCD，即可证得△DEC∽△FDC；
（2）由F为AD的中点，在矩形ABCD中，AD∥BC，可得△DFE∽△BCE，即可求得FE：FC=1：3，易证得△ABF≌△DCF（SAS），可得FB=FC，继而求得答案；
（3）首先设EF=x，则FC=3x，由△DEC∽△FDC，即可求得x的值，继而求得答案．

解答：（1）证明：在矩形ABCD中，∠FDC=90°，CF⊥BD，
∴∠DEC=∠FDC=90°，
∵∠DCE=∠FCD，
∴△DEC∽△FDC；

（2）解：∵F为AD的中点，在矩形ABCD中，AD∥BC，
∴△DFE∽△BCE，
∴FE：EC=FD：BC=FD：AD=1：2，
∴FE：FC=1：3，
在△ABF和△DC中，

AF=FD ∠A=∠FDC=90° AB=DC

，
∴△ABF≌△DCF（SAS），
∴FB=FC，
∴sin∠FBD=EF：BF=EF：FC=

1

3

；

（3）解：设EF=x，则FC=3x，
∵△DEC∽△FDC，
∴

CE

CD

=

CD

FC

，
即可得：6x²=12，
解得：x=±

2

（负值舍去），
则CF=3

2

，
在Rt△CFD中，DF=

FC2-CD2

=

6

，
在矩形ABCD中，BC=AD=2DF=2

6

．

点评：此题考查了相似三角形的判定与性质、矩形的性质以及勾股定理等知识．此题难度适中，注意掌握数形结合思想与方程思想的应用．