题目内容
9.计算:(1)$\sqrt{25}$-$\root{3}{27}$+$\sqrt{\frac{1}{4}}$;
(2)$\sqrt{(-2)^{2}}$+|$\sqrt{2}$-1|-($\sqrt{2}$+1).
(3)(-$\frac{1}{2}$)2+$\frac{3}{4}$-(2-$\sqrt{3}$)+|2-$\sqrt{3}$|
分析 (1)直接利用算术平方根以及立方根的定义化简进而求出答案;
(2直接利用二次根式的性质以及利用绝对值的性质、去括号法则分别化简求出答案;
(3)直接利用绝对值的性质、去括号法则分别化简求出答案.
解答 解:(1)原式=5-3+$\frac{1}{2}$=2$\frac{1}{2}$;
(2)原式=2+$\sqrt{2}$-1-$\sqrt{2}$-1,
=0;
(3)原式=$\frac{1}{4}$+$\frac{3}{4}$-2+$\sqrt{3}$+2-$\sqrt{3}$,
=1.
点评 此题主要考查了实数运算,正确化简各数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图,一个质点在第一象限及x轴,y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第24秒时质点所在位置的坐标是( )
如图,一个质点在第一象限及x轴,y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第24秒时质点所在位置的坐标是( )
 如图,一个质点在第一象限及x轴,y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第24秒时质点所在位置的坐标是( )
如图,一个质点在第一象限及x轴,y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第24秒时质点所在位置的坐标是( )| A. | (0,5) | B. | (5,0) | C. | (0,4) | D. | (4,0) |
14. 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )| A. | 90° | B. | 120° | C. | 60° | D. | 30° |
3.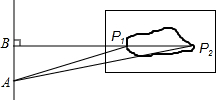 如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )
 如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )| A. | 线段AP1的长度 | B. | 线段AP2的长度 | C. | 线段BP2的长度 | D. | 线段BP1的长度 |

 如图所示,课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置应表示为(4,3).”
如图所示,课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置应表示为(4,3).”