题目内容
 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N,交BE于P.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N,交BE于P.(1)设AE=x,四边形ADNM的面积为S,求出S关于x的函数关系式并写出自变量x的取值范围;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
(3)在(2)的情况下,写出
| MF |
| FN |
考点:四边形综合题
专题:
分析:(1)解题的关键是作辅助线ME、FN,证明出来△EBA≌△MNF,把需要解决的问题转化成解直角三角形的问题,利用勾股定理解答.
(2)根据(1)的答案,利用二次函数的最值问题即可求出;
(3)在(2)的条件下,利用全等三角形的性质得到AE=MF=1,AB=FN=2,所以易求
的值.
(2)根据(1)的答案,利用二次函数的最值问题即可求出;
(3)在(2)的条件下,利用全等三角形的性质得到AE=MF=1,AB=FN=2,所以易求
| MF |
| FN |
解答: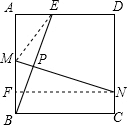 解:(1)如图,连接ME,设MN交BE于P,则MB=ME,MN⊥BE.
解:(1)如图,连接ME,设MN交BE于P,则MB=ME,MN⊥BE.
过N作AB的垂线交AB于F.
在Rt△MBP中,∠MBP+∠BMN=90°,
在Rt△MNF中,∠FNM+∠BMN=90°,
∴∠MBP=∠FNM,即∠ABE=∠FNM
在△EBA与△MNF中,
,
∴△EBA≌△MNF(ASA),
∴MF=AE=x.
在Rt△AME中,AE=x,ME=MB=AB-AM=2-AM,则由勾股定理得到:(2-AM)2=x2+AM2.
整理,得
4-4AM+AM2=x2+AM2,即4-4AM=x2,
解得 AM=1-
x2.
∴梯形ADNM的面积S=
×AD=
×2
=AM+AF=AM+AM+MF=2AM+AE
=2(1-
x2)+x
=-
x2+x+2
即所求关系式为S=-
x2+x+2;
(2)S=-
x2+x+2=-
(x2-2x+1)+
=-
(x-1)2+
,
故当AE=x=1时,四边形ADNM的面积S的值最大,最大值是
;
(3)由(1)知,△EBA≌△MNF,则MF=AE,AB=FN=2.
由(2)知,AE=1,则MF=1,
故
=
.即
的值是
.
 解:(1)如图,连接ME,设MN交BE于P,则MB=ME,MN⊥BE.
解:(1)如图,连接ME,设MN交BE于P,则MB=ME,MN⊥BE.过N作AB的垂线交AB于F.
在Rt△MBP中,∠MBP+∠BMN=90°,
在Rt△MNF中,∠FNM+∠BMN=90°,
∴∠MBP=∠FNM,即∠ABE=∠FNM
在△EBA与△MNF中,
|
∴△EBA≌△MNF(ASA),
∴MF=AE=x.
在Rt△AME中,AE=x,ME=MB=AB-AM=2-AM,则由勾股定理得到:(2-AM)2=x2+AM2.
整理,得
4-4AM+AM2=x2+AM2,即4-4AM=x2,
解得 AM=1-
| 1 |
| 4 |
∴梯形ADNM的面积S=
| AM+DN |
| 2 |
| AM+AF |
| 2 |
=AM+AF=AM+AM+MF=2AM+AE
=2(1-
| 1 |
| 4 |
=-
| 1 |
| 2 |
即所求关系式为S=-
| 1 |
| 2 |
(2)S=-
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
故当AE=x=1时,四边形ADNM的面积S的值最大,最大值是
| 5 |
| 2 |
(3)由(1)知,△EBA≌△MNF,则MF=AE,AB=FN=2.
由(2)知,AE=1,则MF=1,
故
| MF |
| FN |
| 1 |
| 2 |
| MF |
| FN |
| 1 |
| 2 |
点评:此题的综合性比较强,涉及面较广,涉及到正方形的性质,线段垂直平分线的性质及勾股定理的运用,在解答此题时要连接ME,过N点作AB的垂线再求解.

练习册系列答案
相关题目
下列变形,是因式分解的是( )
| A、x(x-1)=x2-x |
| B、x2-x+1=x(x-1)+1 |
| C、x2-x=x(x-1) |
| D、2a(b+c)=2ab+2ac |
关于x的方程:x+
=c+
的解是x1=c,x2=
,x-
=c-
解是x1=c,x2=-
,则x+
=c+
的解是( )
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
| 1 |
| x-1 |
| 1 |
| c-1 |
A、x1=c,x2=
| ||
B、x1=c-1,x2=
| ||
C、x1=c,x2=
| ||
D、x1=c,x2=
|
 用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,两边分别与DA、DB重合.将三角板绕点D逆时针方向旋转.
用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,两边分别与DA、DB重合.将三角板绕点D逆时针方向旋转.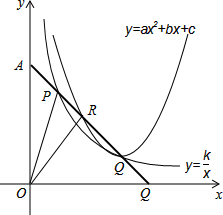 如图,已知点A(0,1),点B(1,0).点P(t,m)是线段AB上一动点,且0<t<
如图,已知点A(0,1),点B(1,0).点P(t,m)是线段AB上一动点,且0<t< 如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3
如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3