��Ŀ����
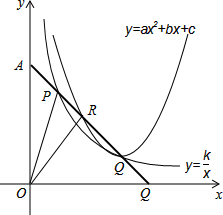 ��ͼ����֪��A��0��1������B��1��0������P��t��m�����߶�AB��һ���㣬��0��t��
��ͼ����֪��A��0��1������B��1��0������P��t��m�����߶�AB��һ���㣬��0��t��| 1 |
| 2 |
| k |
| x |
��1��д���߶�AB����ֱ�ߵı���ʽ��
��2���ú�t�Ĵ���ʽ��ʾk��
��3��������������y=3x2+bx+c���߶�AB����һ������ΪR������POR���������
| 1 |
| 6 |
| k |
| x |
���㣺���κ����ۺ���
ר�⣺
��������1�����ݵ�A�͵�B���������ô���ϵ����ȷ��һ�κ����Ľ���ʽ���ɣ�
��2�����ݵ�P��t��m����AB��y=-x+1��һ�㣬�õ�m=1-t������P��t��1-t��Ȼ�����˫����y=
������P��t��1-t�����õ�k=xy=t��1-t���Ӷ���t��ʾ�������������Ľ���ʽ��
��3����������y=-x+1��y=
���õ�P��t��1-t����Q��1-t��t����Ȼ����ݵ�Q��1-t��t��Ϊ������y=3x2+bx+c�Ķ��㣬�õ�������y=3��x-1+t��2+t���ٴ�����y=-x+1��y=3��x-1+t��2+t����ʾ��Q��1-t��t����R��
-t��t+
�����Ӷ��õ�S��POR=
|
-2t|������S��POR=
ʱȷ��t��ֵ���Ӷ����˫���ߺ������ߵĽ���ʽ��
��2�����ݵ�P��t��m����AB��y=-x+1��һ�㣬�õ�m=1-t������P��t��1-t��Ȼ�����˫����y=
| k |
| x |
��3����������y=-x+1��y=
| t(1-t) |
| x |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |
����⣺��ͼ����1�����߶�AB����ֱ�ߵĽ���ʽΪy=kx+b��
�ߵ�A��0��1������B��1��0����
��
��ã�k=-1��b=1��
���߶�AB����ֱ�ߵı���ʽ��y=-x+1��

��2���ߵ�P��t��m����AB��y=-x+1��һ�㣬
��m=1-t������P��t��1-t��
�֡�˫����y=
������P��t��1-t����
��k=xy=t��1-t��
��˫����y=
��
��3������y=-x+1��y=
��
��ã�x=t��y=1-t����x=1-t��y=t��
��P��t��1-t����Q��1-t��t����
�ߵ�Q��1-t��t��Ϊ������y=3x2+bx+c�Ķ��㣬
��������y=3��x-1+t��2+t��
����y=-x+1��y=3��x-1+t��2+t��
�����ã�3��x-1+t��2+��x-1+t��=0
��ã�x=1-t��y=t����x=
-t��y=t+
��
��Q��1-t��t����R��
-t��t+
����
��S��POR=
|
-2t|��
��S��POR=
ʱ��|
-2t|=
��
���t=
����t=
��
��0��t��
����t=
��
���ʱ��k=t��1-t��=
���ʱ˫����y=
��������y=3��x-
��2+
��
�ߵ�A��0��1������B��1��0����
��
|
��ã�k=-1��b=1��
���߶�AB����ֱ�ߵı���ʽ��y=-x+1��

��2���ߵ�P��t��m����AB��y=-x+1��һ�㣬
��m=1-t������P��t��1-t��
�֡�˫����y=
| k |
| x |
��k=xy=t��1-t��
��˫����y=
| t(1-t) |
| x |
��3������y=-x+1��y=
| t(1-t) |
| x |
��ã�x=t��y=1-t����x=1-t��y=t��
��P��t��1-t����Q��1-t��t����
�ߵ�Q��1-t��t��Ϊ������y=3x2+bx+c�Ķ��㣬
��������y=3��x-1+t��2+t��
����y=-x+1��y=3��x-1+t��2+t��
�����ã�3��x-1+t��2+��x-1+t��=0
��ã�x=1-t��y=t����x=
| 2 |
| 3 |
| 1 |
| 3 |
��Q��1-t��t����R��
| 2 |
| 3 |
| 1 |
| 3 |
��S��POR=
| 1 |
| 2 |
| 2 |
| 3 |
��S��POR=
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 3 |
���t=
| 1 |
| 2 |
| 1 |
| 6 |
��0��t��
| 1 |
| 2 |
| 1 |
| 6 |
���ʱ��k=t��1-t��=
| 5 |
| 36 |
���ʱ˫����y=
| 5 |
| 36x |
| 5 |
| 6 |
| 1 |
| 6 |
���������⿼���˶��κ������ۺ�֪ʶ�������漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�����������йض�������ʱҪע����������������۽����

��ϰ��ϵ�д�
�����Ŀ
��a��b�Ƿ���x2-x-2014=0������ʵ��������a2+2a+3b��ֵΪ��������
| A��2015 | B��2016 |
| C��2017 | D��2018 |
 ��ͼ�����ñ��BE����������DC�ĸ߶ȣ�������BE��Ϊl.2�ף���tanA=
��ͼ�����ñ��BE����������DC�ĸ߶ȣ�������BE��Ϊl.2�ף���tanA=| 3 |
| 4 |
| A��6.3�� | B��7.5�� |
| C��8�� | D��6.5�� |
һ������ε��ڽǺ���1980�㣬��ô�������εı���Ϊ��������
| A��11 | B��12 | C��13 | D��14 |
 ��ͼ����������ABCD�У�AB=2��E��AD����һ�㣨��E���A��D���غϣ���BE�Ĵ�ֱƽ���߽�AB��M����DC��N����BE��P��
��ͼ����������ABCD�У�AB=2��E��AD����һ�㣨��E���A��D���غϣ���BE�Ĵ�ֱƽ���߽�AB��M����DC��N����BE��P��
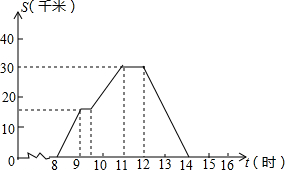 һ������8��00ʱ��С��ȥ�سǹ��������14��00ʱ���ؼң�������ҵľ���Ϊsǧ�ף����ͼ��ش�
һ������8��00ʱ��С��ȥ�سǹ��������14��00ʱ���ؼң�������ҵľ���Ϊsǧ�ף����ͼ��ش�