题目内容
 用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,两边分别与DA、DB重合.将三角板绕点D逆时针方向旋转.
用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,两边分别与DA、DB重合.将三角板绕点D逆时针方向旋转.(1)如图,当三角板的两边分别与菱形的两边AB、CB相交于点E、F时,探求BE、BF、AD的数量关系,并说明理由;
(2)继续旋转三角板,当两边DH、DC分别交AB、BC的延长线于点E、F时,画出旋转后相应的图形,并直接写出BE、BF、AD满足的数量关系式.
考点:菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)由用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,易证得△ADE≌△BDF,继而证得结论;
(2)由题意画出图形,易证得△BDE≌△CDF,继而证得结论.
(2)由题意画出图形,易证得△BDE≌△CDF,继而证得结论.
解答:(1)证明:∵△ABD和△BCD是等边三角形,
∴AD=BD,∠A=∠ADB=∠DBF=60°,
∵∠EDF=60°,
∴∠ADE+∠BDE=∠BDE+∠BDF=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∴BE+BF=AE+BF=AB=AD;
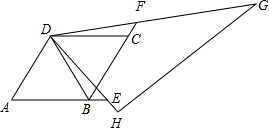 (2)∵△ABD和△BCD是等边三角形,
(2)∵△ABD和△BCD是等边三角形,
∴BD=CD,∠ABD=∠BDC=∠BCD=60°,
∴∠DBE=∠DCF=120°
∵∠EDF=60°,
∴∠BDE+∠CDE=∠CDE+∠CDF=60°
∴∠BDE=∠CDF,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA),
∴BE=CF,
∴BF-BE=BF-CF=BC=AD.
∴AD=BD,∠A=∠ADB=∠DBF=60°,
∵∠EDF=60°,
∴∠ADE+∠BDE=∠BDE+∠BDF=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
|
∴△ADE≌△BDF(ASA),
∴AE=BF,
∴BE+BF=AE+BF=AB=AD;
 (2)∵△ABD和△BCD是等边三角形,
(2)∵△ABD和△BCD是等边三角形,∴BD=CD,∠ABD=∠BDC=∠BCD=60°,
∴∠DBE=∠DCF=120°
∵∠EDF=60°,
∴∠BDE+∠CDE=∠CDE+∠CDF=60°
∴∠BDE=∠CDF,
在△BDE和△CDF中,
|
∴△BDE≌△CDF(ASA),
∴BE=CF,
∴BF-BE=BF-CF=BC=AD.
点评:此题考查了菱形的性质、等边三角形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
已知a、b、c为实数,若a>b,c≠0,则下列结论不一定正确的是( )
| A、a+c>b+c |
| B、c-a<c-b |
| C、ac>bc |
| D、ac2>bc2 |
直线y=-2x+m与直线y=2x-2的交点在第四象限,则m的取值范围是( )
| A、m>-2 | B、m<2 |
| C、-2<m<2 | D、-2≤m≤2 |
 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N,交BE于P.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N,交BE于P. 小霞和爸爸、妈妈到人民公园游玩,回家后,她利用平面直角坐标系画出了公园的景区地图,(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度)
小霞和爸爸、妈妈到人民公园游玩,回家后,她利用平面直角坐标系画出了公园的景区地图,(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度)