题目内容
14.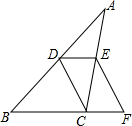 如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=$\frac{1}{2}$BC,连结CD、DE、EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=$\frac{1}{2}$BC,连结CD、DE、EF.(1)求证:四边形CDEF是平行四边形.
(2)若四边形CDEF的面积为8,则△ABC的面积为16.
分析 (1)欲证明四边形CDEF是平行四边形,只需推知DE∥CF,DE=CF;
(2)在四边形CDEF与△ABC中,CF=$\frac{1}{2}$BC,且它们的高相等.
解答  (1)证明:∵如图,在△ABC中,D、E分别是边AB、AC的中点,
(1)证明:∵如图,在△ABC中,D、E分别是边AB、AC的中点,
∴DE∥BC且DE=$\frac{1}{2}$BC.
又∵CF=$\frac{1}{2}$BC,
∴DE=CF,
∴四边形CDEF是平行四边形.
(2)解:∵DE∥BC,
∴△ABC是四边形CDEF的高的2倍,设为h,
又∵CF=$\frac{1}{2}$BC,
∴S△ABC=$\frac{1}{2}$BC•h=CF•h=16,
故答案是:16.
点评 本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.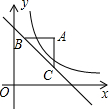 如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
 如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )| A. | 5≤k≤20 | B. | 8≤k≤20 | C. | 5≤k≤8 | D. | 9≤k≤20 |
6.为了解某班学生每天使用零花钱的情况,小明随机查了15名同学,结果如下表:
关于这15名同学每天使用的零花钱,下列说法正确的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是5元 | B. | 极差是4元 | C. | 中位数3元 | D. | 平均数是2.5元 |
 如图,四边形ABCD内接于⊙O,若四边形OABC为平行四边形,则∠D=60度.
如图,四边形ABCD内接于⊙O,若四边形OABC为平行四边形,则∠D=60度. 如图所示的几何体是由五个大小相同的正方体搭建而成的,它的左视图是( )
如图所示的几何体是由五个大小相同的正方体搭建而成的,它的左视图是( )



 在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上.DF=BE.求证:四边形BEDF是矩形.
在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上.DF=BE.求证:四边形BEDF是矩形.