题目内容
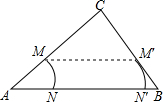 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,M为边AC上一点(不包括点A和C),以点A为圆心,AM长为半径作劣弧交AB于点N,将
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,M为边AC上一点(不包括点A和C),以点A为圆心,AM长为半径作劣弧交AB于点N,将 |
| MN |
 |
| MN |
考点:相似三角形的判定与性质,二次函数的最值,平移的性质
专题:
分析:由平移的性质可知
扫过的面积为一个矩形,过C作C⊥AB,交MM′于H,设矩形的长为y,DH=x,矩形的面积为s,因为MM′∥AB,所以△CMM′∽△CAB,进而得到y和x的关系式,再利用矩形的面积即可得到s和x的函数关系式,根据函数的性质即可求出
扫过的最大面积.
 |
| MN |
 |
| MN |
解答: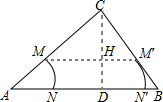 解:过C作C⊥AB,交MM′于H,设矩形的宽为y,DH=x,矩形的面积为s,
解:过C作C⊥AB,交MM′于H,设矩形的宽为y,DH=x,矩形的面积为s,
∵∠C=90°,BC=3,AC=4,
∴AB=
=5,
∴CD=
=2.4,
∵MM′∥AB,
∴△CMM′∽△CAB,
∴
=
,
∴
=
,
∴y=
,
∴s=xy=
•x=-
x2-5x,
∵a<0,
∴s有最大值,为
=-
=3,
故答案为:3.
 解:过C作C⊥AB,交MM′于H,设矩形的宽为y,DH=x,矩形的面积为s,
解:过C作C⊥AB,交MM′于H,设矩形的宽为y,DH=x,矩形的面积为s,∵∠C=90°,BC=3,AC=4,
∴AB=
| AC2+BC2 |
∴CD=
| AC•BC |
| AB |
∵MM′∥AB,
∴△CMM′∽△CAB,
∴
| CH |
| CD |
| MM′ |
| AB |
∴
| 2.4-x |
| 2.4 |
| y |
| 5 |
∴y=
| 60-25x |
| 12 |
∴s=xy=
| 60-25x |
| 12 |
| 25 |
| 12 |
∵a<0,
∴s有最大值,为
| 4ac-b2 |
| 4a |
| 0-25 | ||
|
故答案为:3.
点评:本题考查了平移的性质、勾股定理的运用、相似三角形的判定和性质以及二次函数的性质,解题的关键是读懂题意:可知
扫过的面积为一个矩形,是一道很不错的中考题.
 |
| MN |

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
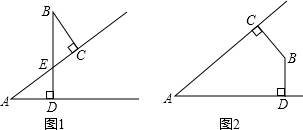
 如图,点A在双曲线y=
如图,点A在双曲线y=