题目内容
20.已知第二象限内一点P(a,b)满足$\left\{\begin{array}{l}{a+1=-t}\\{b-2=2t}\end{array}\right.$.(1)求a,b之间的关系;
(2)求关于x的不等式a(x-3)-2b>0的解集.
分析 (1)根据方程组消去t即可表示出a与b的关系式;
(2)由P为第二象限确定出a与b的正负,即可求出所求不等式的解集.
解答 解:(1)$\left\{\begin{array}{l}{a+1=-t①}\\{b-2=2t②}\end{array}\right.$,
①×2+②得:2a+2+b-2=0,
则a与b的关系式为2a+b=0;
(2)由题意得:a<0,b>0,
不等式去括号得:ax-3a-2b>0,
移项得:ax>3a+2b,
解得:x<$\frac{3a+2b}{a}$.
点评 此题考查了解一元一次不等式,以及点的坐标,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.a14可以写成( )
| A. | a7+a7 | B. | a7•a7 | C. | a5•a8 | D. | a8•a2 |
8.某家具厂销售1套A种款式和2套B种款式的家具的利润为1400元,销售2套A种款式和3套B种款式家具的利润为2400元
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
设甲种板材全部用完时恰好生产A款家具x套,两种款式家具全部售完时的销售利润为y元.
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
| 甲种板材(m2) | 乙种板材(m2) | |
| A款 | 3 | 6 |
| B款 | 5 | 4 |
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
15.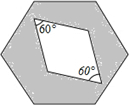 如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{9}$ |
10.一个三角形的两边长为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长是( )
| A. | 11 | B. | 13 | C. | 11或13 | D. | 11和13 |
 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )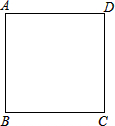 如图,四边形ABCD是一个正方形,
如图,四边形ABCD是一个正方形,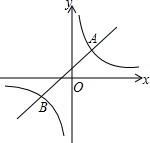 如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于A(2,1)、B(-1,-2)两点.
如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于A(2,1)、B(-1,-2)两点.