题目内容
已知一条射线OA，若从点O再引两条射线OB和OC，使∠AOB=60°，∠BOC=20°，∠AOC的度数为（ ）
| A、40° | B、80° |
| C、20° | D、40°或80° |
考点：角的计算
专题：
分析：若从点O再引两条射线OB和OC，首先弄清有两种情况，即∠AOC=∠AOB+∠BOC或∠AOC=∠AOB-∠BOC，这样就可根据已知条件求出∠AOC的度数．
解答：
解：有两种情况：
第一种情况：如答图①所示：
∠AOC=∠AOB+∠BOC=60°+20°=80°
第二种情况：如答图②所示：
∠AOC=∠AOB-∠BOC=60°-20°=40°
故答案为：∠AOC的度数为80°或40度．
解：有两种情况：第一种情况：如答图①所示：
∠AOC=∠AOB+∠BOC=60°+20°=80°
第二种情况：如答图②所示：
∠AOC=∠AOB-∠BOC=60°-20°=40°
故答案为：∠AOC的度数为80°或40度．
点评：此题考查了角的计算，解题关键：要根据射线OC的位置不同，分类讨论，分别求出∠AOC的度数．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
下列叙述中，正确的是（ ）
| A、点A在直线l上 |
| B、直线的一半是射线 |
| C、延长直线AB到C |
| D、射线OA与射线AO是同一条射线 |
如图，点M（2，2），将一个90°的角尺的直角顶点放在点M处，角尺的两边分别交x轴、y轴正半轴于A、B，AP平分∠OAB，交OM于点P，PN⊥x轴于N，把角尺绕点M旋转时：
如图所示，AE⊥BE，AD⊥DC，CD=BE，∠DAB=∠EAC，求证：AB=AC．
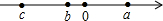有理数a，b，c在数轴上位置如图所示，则下列说法正确的是（ ）| A、a、b、c都表示正数 |
| B、b、c为正数，a为负数 |
| C、a、b、c都表示负数 |
| D、b、c为负数，a为正数 |
如图，∠AOB=40°，OB⊥OC，OD、OE分别平分∠AOB和∠BOC，求∠EOD的度数．