题目内容
已知矩形ABCD中,AB=10cm,AD=4cm,作如下折叠操作.如图1和图2所示,在边AB上取点M,在边AD或边DC上取点P.连接MP.将△AMP或四边形AMPD沿着直线MP折叠得到△A′MP或四边形A′MPD′,点A的落点为点A′,点D的落点为点D′.
探究:
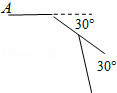
(1)如图1,若AM=8cm,点P在AD上,点A′落在DC上,则∠MA′C的度数为 ;
(2)如图2,若AM=5cm,点P在DC上,点A′落在DC上,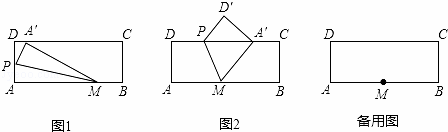
①求证:△MA′P是等腰三角形;
②直接写出线段DP的长.
(3)若点M固定为AB中点,点P由A开始,沿A﹣D﹣C方向.在AD,DC边上运动.设点P的运动速度为1cm/s,运动时间为ts,按操作要求折叠.
①求:当MA′与线段DC有交点时,t的取值范围;
②直接写出当点A′到边AB的距离最大时,t的值;
发现:
若点M在线段AB上移动,点P仍为线段AD或DC上的任意点.随着点M位置的不同.按操作要求折叠后.点A的落点A′的位置会出现以下三种不同的情况:
不会落在线段DC上,只有一次落在线段DC上,会有两次落在线段DC上.
请直接写出点A′由两次落在线段DC上时,AM的取值范围是 .
考点: 几何变换综合题.
分析: (1)根据折叠的性质得出三角形全等,进而分析AM=A′M=8=2MN,利用含30°角的直角三角形的性质解答即可;
(2)①根据矩形的性质和翻折的性质得出∠A′PM=∠A′MP,再利用等角对等边得出等腰三角形,②根据等腰三角形中边之间的关系得出线段的长度即可;
(3)①根据勾股定理得出t的取值范围;②利用矩形的性质作图进行解答.
解答: 解:(1)过点M作MN⊥DC,

∵四边形ABCD是矩形,
∴MN=BC=4,
∵将△AMP沿着直线MP折叠得到△A′MP,
∴AM=A′M=8=2MN,
∴在Rt△A′MN中,∠MA′C=30°;
故答案为:30°;
(2)①∵A′P与AM是矩形ABCD的对边CD,AB的一部分,
∴A′P∥AM,
∴∠A′PM=∠AMP,
由翻折的性质得:∠AMP=∠A′MP,
∴∠A′PM=∠A′MP,
∴A′P=A′M,
∴△MA′P是等腰三角形;
②∵△MA′P是等腰三角形,
∴PM=AM=A′M=5,
∵DA=4,
∴DP=5﹣2=3
∴线段DP的长是3cm;
(3)①当点P在AD上,点A′落在DC上时,如图1所示,
过点M作MN⊥DC交DC于点N,
则四边形AMND为矩形,DN=AM=5cm,MN=4cm,
设AP为xcm,则由翻折的性质得:
AM=A′M=5cm,AP=A′P=xcm,
在Rt△A′MN中,A′N= cm,
cm,
∴DA′=DN﹣A′N=5﹣3=2(cm),
在Rt△A′PD中,
A′P2=A′D2+PD2,
即:x2=22+(4﹣x)2,
解得:x=2.5,
此时t=2.5s;
当点P在AD上,点A′落在DC上时,如图1,
可知DP=3cm,此时,t=7s,
当MA′与DC有交点时,t的取值范围是:2.5≤t≤7,
②当点A′到边AB的距离最大时,
即A′M⊥AB时,t的值为5s,
发现:当点A的落点A′,在以M为圆心,MA为半径的圆上,当圆M与线段CD有唯一交点时,如图2所示,

此时AM=4cm,
当圆M交线段CD于点C时,如图3所示

AM=5.8cm,
所以:4<AM≤5.8,
故答案为:4<AM≤5.8

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( ) B.
B. 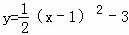 C.
C.  D.
D. 

 ,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )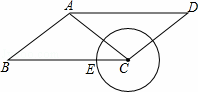
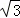 )是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=
)是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=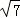 ;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).
;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).
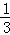 ,则黄球的个数为( )
,则黄球的个数为( )