题目内容
16.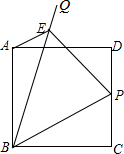 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )| A. | BP•BE=2$\sqrt{2}$ | B. | BP•BE=4$\sqrt{2}$ | C. | $\frac{BE}{BP}$=$\sqrt{2}$ | D. | $\frac{BE}{BP}$=$\frac{3\sqrt{2}}{2}$ |
分析 连接AP,作EM⊥PB于M,根据S△PBE=S△ABP=$\frac{1}{2}$S正方形ABCD=2即可解决问题.
解答 解: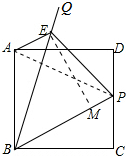 如图,连接AP,作EM⊥PB于M.
如图,连接AP,作EM⊥PB于M.
∵AE∥PB,
∴S△PBE=S△ABP=$\frac{1}{2}$S正方形ABCD=2,
∴$\frac{1}{2}$•PB•EM=2,
∵∠EBM=45°,∠EMB=90°,
∴EM=$\frac{\sqrt{2}}{2}$BE,
∴$\frac{1}{2}$•PB•$\frac{\sqrt{2}}{2}$BE=2,
∴PB•BE=4$\sqrt{2}$.
故选B.
点评 本题考查正方形的性质、平行线的性质等知识,解题的关键是发现△PBE的面积是定值,题目有一定难度,属于中考选择题中的压轴题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
6.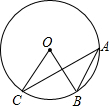 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
7.下列运算正确的是( )
| A. | a•a2=a2 | B. | a+2a=3a | C. | (2a)2=2a2 | D. | (x+2)(x-3)=x2-6 |
4.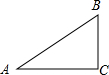 如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
 如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
11.下列计算正确的是( )
| A. | x2+x3=x5 | B. | x2•x3=x6 | C. | x6÷x3=x3 | D. | (x3)2=x9 |
5.把多项式x3-xy2分解因式,下列结果正确的是( )
| A. | x(x+y)2 | B. | x(x-y)2 | C. | x(x-y)(x+y) | D. | x(x2-y2) |
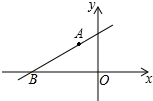 如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.