题目内容
6.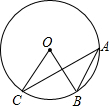 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
分析 由⊙O经过A,B,C三点,∠BOC=60°,根据圆周角定理,即可求得∠A的度数,继而求得答案.
解答 解:∵∠BOC=60°,
∴∠A=$\frac{1}{2}$∠BOC=30°,
∴sinA=sin30°=$\frac{1}{2}$.
故选D.
点评 此题考查了圆周角定理以及特殊角的三角函数问题.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
14.下列运算正确的是( )
| A. | a3+a3=a6 | B. | a2•a2=a4 | C. | (2a)4=2a4 | D. | a6÷a3=a2 |
11.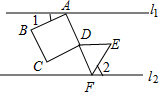 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )| A. | 30° | B. | 60° | C. | 45° | D. | 15° |
18. 在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )
在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )
 在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )
在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{\sqrt{10}}{10}$ |
15.下列现象是平移的是( )
| A. | 钟摆的运动 | B. | 方向盘的转动 | C. | 汽车车轮的运动 | D. | 电梯的升降 |
16.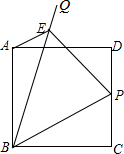 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )| A. | BP•BE=2$\sqrt{2}$ | B. | BP•BE=4$\sqrt{2}$ | C. | $\frac{BE}{BP}$=$\sqrt{2}$ | D. | $\frac{BE}{BP}$=$\frac{3\sqrt{2}}{2}$ |
