题目内容
1.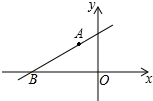 如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.
分析 根据点B的坐标确定kx+b>0时x的范围,根据图象和y=-2x经过点A(-1,2),确定kx+b<-2x时,x的范围.
解答 解:∵B(-$\sqrt{7}$,0)
∴x>-$\sqrt{7}$时,kx+b>0,
∵y=-2x经过点A(-1,2),
∴当x<-1时,kx+b<-2x,
则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1,
故答案为:-$\sqrt{7}$<x<-1.
点评 本题考查的是一次函数与一元一次不等式,一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
11.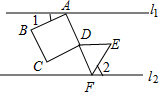 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )| A. | 30° | B. | 60° | C. | 45° | D. | 15° |
9. 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
16.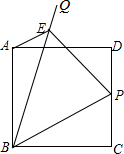 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )| A. | BP•BE=2$\sqrt{2}$ | B. | BP•BE=4$\sqrt{2}$ | C. | $\frac{BE}{BP}$=$\sqrt{2}$ | D. | $\frac{BE}{BP}$=$\frac{3\sqrt{2}}{2}$ |
10. 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | π | C. | π-$\sqrt{3}$ | D. | $\sqrt{3}$ |
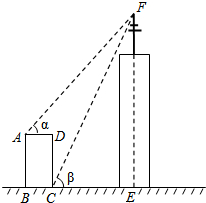 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.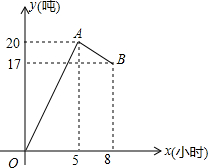 某仓库有甲,乙,丙三辆运货车,每辆车只负责进货或出货,甲车的运输量为每小时6吨,如图是从早晨开始库存量y(吨)与时间x(小时)的函数图象,OA段只有甲乙两车一起工作,AB段只有乙丙两车一起工作.
某仓库有甲,乙,丙三辆运货车,每辆车只负责进货或出货,甲车的运输量为每小时6吨,如图是从早晨开始库存量y(吨)与时间x(小时)的函数图象,OA段只有甲乙两车一起工作,AB段只有乙丙两车一起工作.