题目内容
4.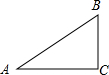 如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 利用锐角三角函数的定义求解,sinA为∠A的对边比斜边,求出即可.
解答 解:∵∠C=90°,AB=5,AC=4,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3,
∴sinA=$\frac{BC}{AB}=\frac{3}{5}$.
故选D.
点评 此题主要考查了锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.下列运算正确的是( )
| A. | a3+a3=a6 | B. | a2•a2=a4 | C. | (2a)4=2a4 | D. | a6÷a3=a2 |
15.下列现象是平移的是( )
| A. | 钟摆的运动 | B. | 方向盘的转动 | C. | 汽车车轮的运动 | D. | 电梯的升降 |
19.下列运算正确的是( )
| A. | a2×a3=a6 | B. | a2+a2=2a4 | C. | a8÷a4=a4 | D. | (a2)3=a5 |
9. 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
16.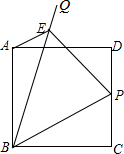 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )| A. | BP•BE=2$\sqrt{2}$ | B. | BP•BE=4$\sqrt{2}$ | C. | $\frac{BE}{BP}$=$\sqrt{2}$ | D. | $\frac{BE}{BP}$=$\frac{3\sqrt{2}}{2}$ |
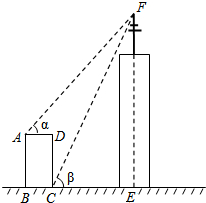 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.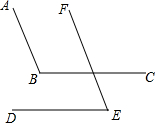 如图,若AB∥EF,BC∥DE,则∠B+∠E=180°.
如图,若AB∥EF,BC∥DE,则∠B+∠E=180°.