题目内容
6.如果x4-x3+kx2-2kx-2能分解为两个整系数的二次因式,试求k的值.分析 由于(x2)2-x3+kx2-2kx-2能分解成两个整数系数的二次因式的积,可设(x2)2-x3+kx2-2kx-2=(x2+ax-1)(x2+bx+2)或(x2+ax+1)(x2+bx-2).展开利用对应项的系数相等即可得出.
解答 解:∵(x2)2-x3+kx2-2kx-2能分解成两个整数系数的二次因式的积,
∴可设(x2)2-x3+kx2-2kx-2=(x2+ax-1)(x2+bx+2)或(x2+ax+1)(x2+bx-2).
①(x2+ax-1)(x2+bx+2)=x4+(a+b)x3+(1+ab)x2+(2a-b)x-2,
∴$\left\{\begin{array}{l}{a+b=-1}\\{1+ab=k}\\{2a-b=-2k}\end{array}\right.$,
解得k=1或k=$\frac{7}{4}$.
②(x2+ax+1)(x2+bx-2)=x4+(a+b)x3+(ab-1)x2+(b-2a)x-2,
∴$\left\{\begin{array}{l}{a+b=-1}\\{ab-1=k}\\{b-2a=-2k}\end{array}\right.$,
解得k=-1或k=-$\frac{7}{4}$.
综上可得:k的值为1或$\frac{7}{4}$或-1或-$\frac{7}{4}$.
点评 此题考查了因式分解的应用,理解题意,根据原式分解为两个整系数的二次因式,利用待定系数法求得答案即可.

练习册系列答案
相关题目
11.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{0.5}$ | B. | $\sqrt{5}$ | C. | $\sqrt{50}$ | D. | $\sqrt{{a}^{2}b}$ |
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | $\sqrt{9}$=3 | D. | 2+$\sqrt{5}$=2$\sqrt{5}$ |
 如图,在?ABCD中,E是BC边上一点,试在AD边上找一点F,使四边形AECF是平行四边形,并说明理由.
如图,在?ABCD中,E是BC边上一点,试在AD边上找一点F,使四边形AECF是平行四边形,并说明理由.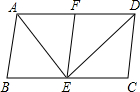 如图,已知平行四边形ABCD,沿着DE折叠后点C落在AD边上的F处.
如图,已知平行四边形ABCD,沿着DE折叠后点C落在AD边上的F处. 如图,Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,则圆O的半径为2cm.
如图,Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,则圆O的半径为2cm.