题目内容
1.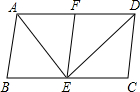 如图,已知平行四边形ABCD,沿着DE折叠后点C落在AD边上的F处.
如图,已知平行四边形ABCD,沿着DE折叠后点C落在AD边上的F处.(1)求证:CD∥EF;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
分析 (1)首先根据平行四边形的性质可得AD∥CB,然后再证明CD=EC,再根据折叠可得DC=FD,进而可得DF=EC,从而可得四边形EFDC是平行四边形,根据平行四边形的性质可得CD∥EF;
(2)首先证明AB=BE,再根据三角形内角和可得∠AEB的度数,根据平行线的性质可得∠DAE的度数.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠1=∠3,
根据折叠可得∠1=∠2,DC=FD,
∴∠2=∠3,
∴CD=EC,
∴DF=EC,
∴四边形EFDC是平行四边形,
∴CD∥EF;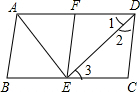
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥CB,
∵CD=EC,BE=CE,
∴∠BEA=∠BAE=(180°-80°)÷2=50°,
∵AD∥BC,
∴∠DAE=∠AEB=50°.
点评 此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形对边平行,一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
13.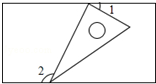 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )| A. | 155° | B. | 135° | C. | 125° | D. | 115° |
10.2015的倒数是( )
| A. | -2015 | B. | $-\frac{1}{2015}$ | C. | $\frac{1}{2015}$ | D. | 2015 |
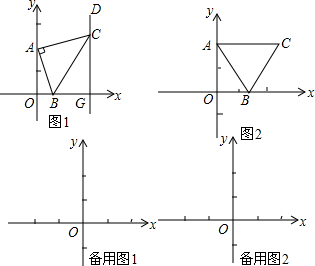
 在同一平面直角坐标系中画出下列函数的图象,并指出它们的共同之处.
在同一平面直角坐标系中画出下列函数的图象,并指出它们的共同之处.