题目内容
已知关于x的方程x2+(a-2)x+a+1=0的两实根x1、x2满足x12+x22=4,则实数a= .
考点:根与系数的关系
专题:探究型
分析:先根据根与系数的关系得出两根之积与两根之和,代入x12+x22=4进行计算即可.
解答:解:∵关于x的方程x2+(a-2)x+a+1=0的两实根为x1、x2,
∴△=(a-2)2-4(a+1)≥0,即a(a-8)≥0,
∴当a≥0时,a-8≥0,即a≥8;
当a<0时,a-8<0,即a<8,所以a<0.
∴a≥8或a<0,
∴x1+x2=2-a,x1•x2=a+1,
∵x12+x22=4,(x1+x2)2-2x1•x2=(2-a)2-2(a+1)=4,
∴(x1+x2)2-2x1•x2=(2-a)2-2(a+1)=4,解得a=3±
.
∵3<
<4,
∴6<3+
<7(不合题意舍去),3-
<0;
∴a=3-
.
故答案为:a=3-
.
∴△=(a-2)2-4(a+1)≥0,即a(a-8)≥0,
∴当a≥0时,a-8≥0,即a≥8;
当a<0时,a-8<0,即a<8,所以a<0.
∴a≥8或a<0,
∴x1+x2=2-a,x1•x2=a+1,
∵x12+x22=4,(x1+x2)2-2x1•x2=(2-a)2-2(a+1)=4,
∴(x1+x2)2-2x1•x2=(2-a)2-2(a+1)=4,解得a=3±
| 11 |
∵3<
| 11 |
∴6<3+
| 11 |
| 11 |
∴a=3-
| 11 |
故答案为:a=3-
| 11 |
点评:本题考查的是根与系数的关系,熟记x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
是解答此题的关键.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
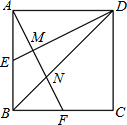 如图,正方形ABCD的边长为2
如图,正方形ABCD的边长为2| 15 |
| A、8 | ||
| B、12 | ||
C、
| ||
| D、15 |
已知四边形ABCD的对角线AC与BD相交于O,给出下列四个论断:①OA=OC;②AB=CD;③∠BAD=∠DCB;④AD∥BC.从中选择两个作为条件,以“四边形ABCD为平行四边形”作为结论,得到的6个命题中,真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若x=
+
,y=
-
,则
=( )
| a |
| b |
| a |
| b |
| 1 |
| xy |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,△ACB中∠ACB=90°,∠A=40°.将△ACB绕点C顺时针旋转得到△DCE,边DE恰好经过点B,则∠DCB的度数为
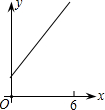
如图,△ACB中∠ACB=90°,∠A=40°.将△ACB绕点C顺时针旋转得到△DCE,边DE恰好经过点B,则∠DCB的度数为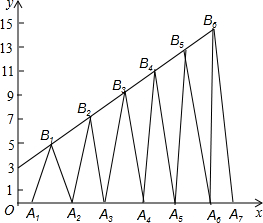 已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=
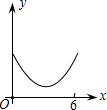
已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=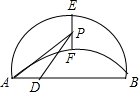 如图弧AEB与弧AFB有公共弦AB=6,D是弦AB上的一点,AD=x,点E、F分别是弧AEB与弧AFB的中点,P是EF上的中点,y=AP2-DP2,则y与x的函数关系式是( )
如图弧AEB与弧AFB有公共弦AB=6,D是弦AB上的一点,AD=x,点E、F分别是弧AEB与弧AFB的中点,P是EF上的中点,y=AP2-DP2,则y与x的函数关系式是( )