题目内容
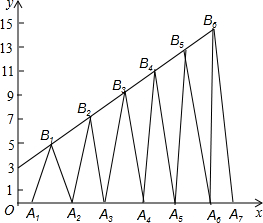 已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=
已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=考点:一次函数综合题
专题:规律型
分析:根据一次函数图象上点的坐标特征求得点B1、B2、B3的纵坐标,然后由三角形的面积公式求得S1,S2…Sn;由此规律即可求得S2011-S2009的值.
解答:解:∵B1(1,y1)、B2(2,y2)、B3(3,y3)…在直线y=2x+3上,
∴y1=2×1+3=5,y2=2×2+3=7,y3=2×3+3=9,yn=2n+3(n∈N);
又∵OA1=a(0<a<1),
∴S1=
×2×(1-a)×5=5(1-a);
S2=
×2×[2-a-2×(1-a)]×7=7a;
S3=
×2×{3-a-2×(1-a)-2×[2-a-2×(1-a)]}×9=9(1-a);
…
Sn=(2n+3)(1-a)(n是奇数);
∴S2011-S2009=(2×2011+3)(1-a)-(2×2009+3)(1-a)=4(1-a);
故答案是:4(1-a).
∴y1=2×1+3=5,y2=2×2+3=7,y3=2×3+3=9,yn=2n+3(n∈N);
又∵OA1=a(0<a<1),
∴S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
S3=
| 1 |
| 2 |
…
Sn=(2n+3)(1-a)(n是奇数);
∴S2011-S2009=(2×2011+3)(1-a)-(2×2009+3)(1-a)=4(1-a);
故答案是:4(1-a).
点评:本题考查了一次函数综合题.解答此题的关键是根据已知条件找出n为奇数时,三角形面积的通式Sn=(2n+3)(1-a)(n是奇数).

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
设一个凸多边形的边数为奇数,除去两个内角外,其余内角和为2390°,则除去的这两内角的度数和为( )
| A、130° | B、300° |
| C、310° | D、490° |
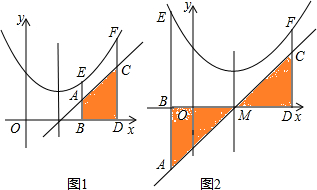 已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.
已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积. 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,sin∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,sin∠ABO=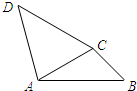 如图,在四边形ABCD中,∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,若AB=2,则CD的长为
如图,在四边形ABCD中,∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,若AB=2,则CD的长为