题目内容
 如图,?ABCD中,E是BC的中点,AE=9,BD=12,AD=10.
如图,?ABCD中,E是BC的中点,AE=9,BD=12,AD=10.(1)求证:AE⊥BD;
(2)求?ABCD的面积.
考点:平行四边形的性质
专题:
分析:(1)先证明△AFD∽△EFB,进而算出EF=3,BF=4,BE=5,再证明△BFE是直角三角形,从而证得AE⊥BD;
(2)再求解△ABE的面积,进一步求出平行四边形的面积.进而得到△BAD的面积,最后求得平行四边形ABCD的面积.
(2)再求解△ABE的面积,进一步求出平行四边形的面积.进而得到△BAD的面积,最后求得平行四边形ABCD的面积.
解答:解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AFD∽△EFB,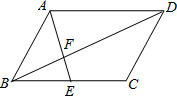
∵E是BC的中点,
∴BE=
AD,
∴
=
=
,
∵AE=9,BD=12,AD=10,
∴EF=3,BF=4,BE=5,
∵32+42=52,
∴△BFE是直角三角形,
∴AE⊥BD;
(2)∵AE⊥BD,
∴S△BEF=
•BF•EF=6,
又∵S△BFE:S△ABF=EF:FA=1:2,
∴S△ABF=12,得S△ABE=18,
∵E是BC的中点,
∴S?ABCD=4S△ABE=72.
∴AD∥BC,
∴△AFD∽△EFB,

∵E是BC的中点,
∴BE=
| 1 |
| 2 |
∴
| FE |
| AF |
| BE |
| AD |
| 1 |
| 2 |
∵AE=9,BD=12,AD=10,
∴EF=3,BF=4,BE=5,
∵32+42=52,
∴△BFE是直角三角形,
∴AE⊥BD;
(2)∵AE⊥BD,
∴S△BEF=
| 1 |
| 2 |
又∵S△BFE:S△ABF=EF:FA=1:2,
∴S△ABF=12,得S△ABE=18,
∵E是BC的中点,
∴S?ABCD=4S△ABE=72.
点评:此题主要考查了相似三角形的判定与性质,勾股定理逆定理,平行四边形的性质,关键是证出△BFE是直角三角形,算出△ABE的面积.

练习册系列答案
相关题目
 如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )
如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )| A、30° | B、45° |
| C、60° | D、不能确定 |
下列说法不正确的是( )
| A、经过平移,图形的形状和大小都不改变 |
| B、经过旋转,图形的形状和大小发生了改变 |
| C、轴对称图形,对称轴两旁的部分一定完全重合 |
| D、平移中,图形上每个点沿直线运动 |
 作图题:作线段AB的垂直平分线(尺规作图,不写作法,保留作图痕迹)
作图题:作线段AB的垂直平分线(尺规作图,不写作法,保留作图痕迹) 如图,已知△ABE≌△ACD,求证:∠1=∠2.
如图,已知△ABE≌△ACD,求证:∠1=∠2. 如图所示,四边形EFGH是四边形ABCD平移得到的.找出图中平行且相等的四条线段和一组全等的四边形.
如图所示,四边形EFGH是四边形ABCD平移得到的.找出图中平行且相等的四条线段和一组全等的四边形. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交EF于点F,BC=6.求CF的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交EF于点F,BC=6.求CF的长.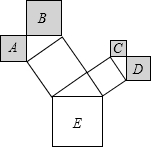 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是