Question

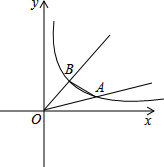如图，已知∠AOB在平面直角坐标系的第一象限中，且∠AOB=30°，其两边分别交反比例函数y=

3

x

在第一象限内的图象于A、B两点，连结AB，当∠AOB绕点O转动时，线段AB的最小值为（　　）

• A、

  3

  -1
• B、2

  3

  -2
• C、

  3

• D、

  6

  -

  2

Answer 1

考点：反比例函数综合题

专题：综合题

分析：由题意，根据对称性，可知当∠AOx=30°时，线段AB的最小，求出A，B的坐标，即可得出结论．

解答：解：由题意，根据对称性，可知当∠AOx=30°时，线段AB的最小，
此时直线OA的方程为y=

3

3

x，与y=

3

x

联立，得

y= 3 3 x y= 3 x

，
解得：

x= 3 y=1

或

x=1 y= 3

，即A（

3

，1），B（1，

3

），
∴|AB|=

( 3 -1)2+(1- 3 )2

=

6

-

2

．
故选D

点评：此题属于反比例函数综合题，涉及的知识有：直线的点斜式方程，一次函数与反比例函数图象的交点，以及两点间的距离公式，根据题意得出当∠AOx=30°时，线段AB的最小是解本题的关键．