题目内容
11. 如图,一次函数y=kx+b(k≠0)和反比例函数y=$\frac{m}{x}$(m≠0)交于点A(4,1)与点B(-1,n).
如图,一次函数y=kx+b(k≠0)和反比例函数y=$\frac{m}{x}$(m≠0)交于点A(4,1)与点B(-1,n).(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
分析 (1)把点A(4,1)与点B(-1,n)代入反比例函数y=$\frac{m}{x}$得到m=4,即反比例函数的解析式为y=$\frac{4}{x}$,把点A(4,1)与点B(-1,-4)代入一次函数y=kx+b,得到$\left\{\begin{array}{l}{1=4k+b}\\{-4=-k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$得到一次函数解析式为y=x-3;
(2)根据三角形的面积公式即可得到结论;
(3)由图象即可可得结论.
解答 (1)解:∵点A(4,1)与点B(-1,n)在反比例函数y=$\frac{m}{x}$(m≠0)图象上,
∴m=4,即反比例函数的解析式为y=$\frac{4}{x}$,
当x=1时,n=-4,即B(-1,-4),
∵点A(4,1)与点B(-1,-4)在一次函数y=kx+b(k≠0)图象上,
∴$\left\{\begin{array}{l}{1=4k+b}\\{-4=-k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$
∴一次函数解析式为y=x-3;
(2)解:对于y=x-3,当y=0时,x=3,
∴C(3,0)
∴S△AOB=S△AOC+S△BOC=$\frac{15}{2}$;
(3)解:由图象可得,当-1<x<0或x>4时,一次函数的值大于反例函数的值.
点评 本题考查的是反比例函数与一次函数的交点问题及三角形的面积公式,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
1. 用一个平面去截如图的长方体,截面不可能为( )
用一个平面去截如图的长方体,截面不可能为( )
 用一个平面去截如图的长方体,截面不可能为( )
用一个平面去截如图的长方体,截面不可能为( )| A. |  | B. |  | C. |  | D. |  |
20.将二次函数表达式y=x2-2x+3用配方法配成顶点式正确的是( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+4 | C. | y=(x-1)2-2 | D. | y=(x+2)2-2 |
 如图,已知点C为AB上一点,AC=18cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=18cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.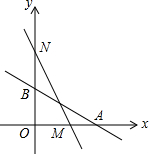 如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动. 河上有一座桥孔为抛物线形的拱桥,水面宽为6米时,水面离桥孔顶部3米.把桥孔看成一个二次函数的图象,以桥孔的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图所示的平面直角坐标系.
河上有一座桥孔为抛物线形的拱桥,水面宽为6米时,水面离桥孔顶部3米.把桥孔看成一个二次函数的图象,以桥孔的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图所示的平面直角坐标系.